Equacions exponencials i logarítmiques 1. Equacions exponencials Una equació exponencial és aquella en la que apareixen exponencials, és a dir, potències que tenen la incògnita, x, en els exponents. En aquesta pàgina resoldrem equacions exponencials sense emprar logaritmes. El mètode de resolució consisteix en aconseguir una igualtat entre dues exponencials amb la mateixa base per poder igualar els seus exponents. Aplicarem les propietats de les potències. Exemple 1: Si escrivim 27 com...

Equacions de segon grau completes i incompletes Una equació de segon grau és una equació polinòmica de grau 2, és a dir, el major grau dels monomis és 2, o siga, x al quadrat. Com que l'equació és de grau 2, tindrà, com a molt, dues arrels (solucions) distintes. Tota equació de segon grau es pot escriure en la forma Si ningun dels coeficients, a,b i c és zero, és a dir, direm que l'equació és completa. Si no és així (si b ó c és 0), direm que és incompleta. 1. Equació completa Les...

Si conocemos dos lados de un triángulo rectángulo, podemos calcular el otro lado aplicando el teorema de Pitágoras. Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno. El coseno de un ángulo α se define como el cociente del lado contiguo al ángulo α y la hipotenusa. De forma análoga, el seno de α se define como el cociente del lado opuesto al ángulo α y la hipotenusa. Nota: si...

Intervalos Definimos el intervalo [a,b] siendo a<b como el conjunto formado por todos los números (reales) que son mayores o iguales que a y menores o iguales que b. Los números a y b se denominan extremos del intervalo [a,b]. Representación en la recta real del intervalo [a,b]: Ejemplos: El número 3 está en el intervalo [0,5] porque 3 es mayor o igual que 0 y menor o igual que 5. El número 6 no está en el intervalo [0,5] porque es mayor o igual que 0 pero no es menor o ...

Hola, en el siguiente enlace pueden encontrar ejercicios interactivos de matemáticas. Son ejercicios con auto-corrección de álgebra, operaciones entre enteros, tablas de multiplicar.... Además, en la misma web Matesfacil.com, pueden encontrar apuntes y problemas resueltos de matemáticas para secundaria y bachillerato. Un saludo. Enlace: Ejercicios interactivos Otros: Problemas y Ecuaciones Ecuaciones Resueltas

Cálculo de Ráices Cuadradas Vamos a ver las partes de una raíz cuadrada y el algoritmo (método) para calcular la raíz cuadrada de un número. Partes de una raíz cuadrada: El radicando es el número cuya raíz queremos calcular. Es decir, si b es el radicando y aes la raíz de b, entonces a al cuadrado es b. El radicando se escribe bajo el signo radical. Por ejemplo, si el radicando es 4, entonces la raíz cuadrada es 2 ya que 2 al cuadrado es 4. Si la raíz cuadrada no es número exacto (o se...

Pythagoren Theorem Pythagoras' Theorem: Given a right triangle with sides a and b and a hypotenuse h (the side opposite the right angle). Then, Remember that... triangle is a right-angled triangle because it has a right angle, an angle of 90º or π / 2 radians The hypotenuse is the opposite side as the right angle. Note: h is always bigger than the other sides, as shows h > a and h > b. The Pythagoras theorem is one of the most known results in mathematics and also one...

1. Definición Informalmente, seafuna función biyectiva. Entonces, su función inversa,g,es la función que proporciona las anti-imágenes del recorrido def. Por ejemplo, sif(a) = b, entoncesg(b) = a. Ejemplo: La inversa de la funciónf(x) = 2xesg(x) = x/2. Veamos quegproporciona las anti-imágenes def: f(2) = 2·2 = 4, g(4) = 4/2 = 2 f(3) = 2·3 = 6, g(6) = 6/2 = 3 f(-10) = 2·(-10) = -20, g(-20) = -20/2 = -10 Normalmente, la función inversa defse denota porf^1, pero por comodidad, ...

Asíntotas de funciones Informalmente, decimos que la función f tiene una asíntota en la recta r del plano real si la gráfica de f se acerca indefinidamente a la recta r. Ejemplo: La función f(x) = 1/x tiene asíntotas en las rectas y = 0 y x = 0: Las asíntotas pueden ser horizontales, verticales u oblicuas. La recta horizontal y = a es una asíntota horizontal de f si el límite de f(x) cuando x tiende a +infinito ó a -infinito es a. Ejemplo 1: La función exponencial f(x) = e^x tiene una ...

Exercicis Resolts de Matemàtiques Índex: Nombres: Mínim comú múltiple Màxim comú divisor Fraccions: Introducció a les fraccions Suma i resta de fraccions Multiplicació i divisió de fraccions Fracció generatriu de nombres decimals Fracció mixta o nombre mixt Potències: Calcular potències i simplificar expressions amb potències emprant les seves propietats Equacions de primer grau: Resoldre equacions Problems de plantejar equacio...

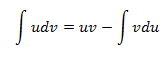
Métodos de Integración Algunas primitivas se obtienen directamente a partir de la tabla de derivadas, este es el caso de las integrales directas o inmediatas, como por ejemplo: Sin embargo, lo habitual es que resolver una integral no sea una tarea fácil, razón por la que existen distintos métodos de integración. Los métodos básicos son: integración por partes integración por sustitución integración de funciones racionales Veamos un ejemplo de cada uno de ellos: 1. Int...

Un porcentaje es una proporción tomando como referencia el número 100. Se expresa con un número seguido del signo %. Ejemplo 1: El 50% es la mitad ya que 50 es la mitad de 100. El 50% de 200 es 100. Ejemplo 2: El veinte por ciento (20%) es la quinta parte ya que 20 es la quinta parte de 100. El 20% de 500 es 100. Ejemplo 3: El 100% es el total ya que 100 es el total de 100. El 100% de 250 es 250. Cálculo de un porcentaje Los porcentajes son siempre relaciones de proporcio...

Os presento el proyecto colaborativo Tertulias con sabor a chocolate “una iniciativa centrada en la comunicación oral, en el diálogo, en la palabra sentida, imaginada, pensada, en la palabra que encuentra oportunidad y espacio para ser hablada y escuchada, en la palabra que, adentrándose en el universo del otro, va tejiendo respuesta...” en la que “...resuena la tradición de las comunidades de investigación fIlosófica, de las comunidades de aprendizaje, de las comunidades dialógicas” (1) Es ...

En el año 2000, Año Mundial de las Matemáticas, se instituyó la celebración del día 12 de mayo como Día Escolar de las Matemáticas por la Federación Española de Sociedades de Profesores de Matemáticas (FESPM). Esta fecha fue elegida en honor a Pedro Puig Adam, nacido el 12 de mayo de 1900 e internacionalmente reconocido en el campo de la enseñanza de las Matemáticas. Las diferentes Sociedades de Profes...

Cuando necesito algún recurso en concreto, lo busco, si lo encuentro, lo añado a mi listado particular.Lo comparto con vosotros.

Una pregunata guía tan sencilla como ésta se puede convertir en un ABP muy interesante para llevar a cabo en un centro de Secundaria, Bachillerato o incluso en algún FP concreto. Esta es lo que nos motivó a mí y a unas cuantas compañeras (IsabelSánchez, Pilar Gregorio, Beatriz Martínez y Ester Alonso) a realizar este proyecto que compartimos con vosotros. Nuestros objetivos, encaminados al conocimiento de lo que consumimos y al disfrute de una dieta saludable de los mismos, se concretaban en...

Wiki dedicada a la investigación sobre Gamificación aplicada a la educación, realizada por profesores y para profesores. El objetivo es elaborar un esquema práctico sobre los pasos necesarios para diseñar un sistema gamificado general que pueda ser personalizado según las necesidades de cada docente y grupo. La estructura general podrá ser completada con la sabiduría atesorada por los miembros de este grupo al aplicar la gamificaci&oacut...

La UOC oferta un MOOC dirigido a los docentes que deseen participar en el proyecto Hands-On ICT con la finalidad principal de crear una actividad aplicable a la realidad del aula utilizando herramientas TIC (learning design studio). La fecha de inicio era ayer, 27 de octubre, pero las inscripciones siguen abiertes. Los materiales están en inglés pero los foros se proponen en diferentes lenguas.

7 Simple steps to setting up Google Hangouts on Air, de Lisa Nielsen. (En inglés)

Se trata de un recurso que ayuda a comprender el muestreo aleatorio simple. Así mismo, se puede utilizar para resolver dicho muestreo.