Asíntotas de funciones
Asíntotas de funciones
Informalmente, decimos que la función f tiene una asíntota en la recta r del plano real si la gráfica de f se acerca indefinidamente a la recta r.
Ejemplo: La función f(x) = 1/x tiene asíntotas en las rectas y = 0 y x = 0:
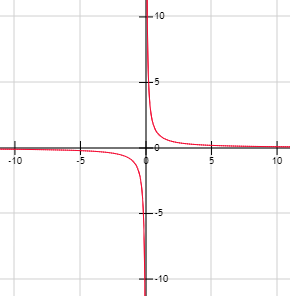
Las asíntotas pueden ser horizontales, verticales u oblicuas.
La recta horizontal y = a es una asíntota horizontal de f si el límite de f(x) cuando x tiende a +infinito ó a -infinito es a.
Ejemplo 1: La función exponencial f(x) = e^x tiene una asíntota horizontal en y = 0, pero sólo por la izquierda (reales negativos):
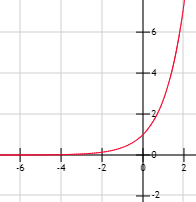
La recta vertical x = a es una asíntota vertical de f si el límite de f por la derecha o por la izquierda de a tiende a infinito.
Ejemplo: La función racional f(x) = 1/x tiene una asíntota vertical por ambos lados en x = 0:

La recta y = ax+b (siendo a distinto de 0) es una asíntota oblicua de f si el límite de f(x) – (ax+b) cuando x tiende a +infinito ó a -infinito es 0.
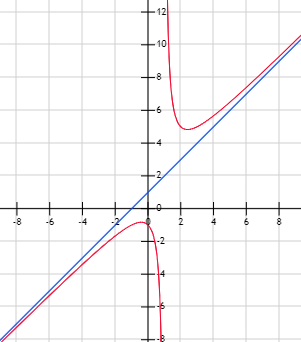
Ejemplo: La función f(x) = (x^2+1)/(x-1) (en color rojo) tiene la asíntota oblicua y = x+1 (en color azul):
Más información y problemas:


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


