Os presento en el siguiente enlace el trabajo de centro con 12 lesson plans elaboradas por el equipo SymbalooEDU del colegio, 12 compañeros que hemos cursado “Aprendizaje personalizado en entornos digitales”. URL: Webmix-Colegio La Merced-Jesuitas-Burgos Centro educativo: La Merced y San Francisco Javier”. Jesuitas. Burgos. El boceto de centro se diseñó siguiendo un mismo hilo conductor en el centro: “El comercio”. De esta forma, los contenidos que se trabajan en los itinerarios giran en...

Equacions exponencials i logarítmiques 1. Equacions exponencials Una equació exponencial és aquella en la que apareixen exponencials, és a dir, potències que tenen la incògnita, x, en els exponents. En aquesta pàgina resoldrem equacions exponencials sense emprar logaritmes. El mètode de resolució consisteix en aconseguir una igualtat entre dues exponencials amb la mateixa base per poder igualar els seus exponents. Aplicarem les propietats de les potències. Exemple 1: Si escrivim 27 com...

Intervalos Definimos el intervalo [a,b] siendo a<b como el conjunto formado por todos los números (reales) que son mayores o iguales que a y menores o iguales que b. Los números a y b se denominan extremos del intervalo [a,b]. Representación en la recta real del intervalo [a,b]: Ejemplos: El número 3 está en el intervalo [0,5] porque 3 es mayor o igual que 0 y menor o igual que 5. El número 6 no está en el intervalo [0,5] porque es mayor o igual que 0 pero no es menor o ...

Hola, en el siguiente enlace pueden encontrar ejercicios interactivos de matemáticas. Son ejercicios con auto-corrección de álgebra, operaciones entre enteros, tablas de multiplicar.... Además, en la misma web Matesfacil.com, pueden encontrar apuntes y problemas resueltos de matemáticas para secundaria y bachillerato. Un saludo. Enlace: Ejercicios interactivos Otros: Problemas y Ecuaciones Ecuaciones Resueltas

Ecuaciones Exponenciales Una ecuación exponencial es aquella en la que aparecen exponenciales, es decir, potencias cuyos exponentes son expresiones en las que aparece la incógnita, x. En esta sección, resolveremos ecuaciones exponenciales sin usar logaritmos. El método de resolución consiste en conseguir una igualdad de exponenciales con la misma base para poder igualar los exponentes. Para ello, utilizaremos las propiedades de las potencias. Ejemplo 1: Escribimos 16 como una potencia ...

Logarithmic Equations and Systems A logarithmic equation is an equation that has an unknown factor in the argument of a logarithm. In reality, the resolution is reduced to the resolution of equations of the same type as the expressions in the arguments (quadratic equations, cubic equations, irrational equations...). Before starting the exercises, let's remember the logarithmic properties: Logarithm of a product: Logarithm of a quotient: Logarithm of a power: Change of base: Use...

1. Definición Informalmente, seafuna función biyectiva. Entonces, su función inversa,g,es la función que proporciona las anti-imágenes del recorrido def. Por ejemplo, sif(a) = b, entoncesg(b) = a. Ejemplo: La inversa de la funciónf(x) = 2xesg(x) = x/2. Veamos quegproporciona las anti-imágenes def: f(2) = 2·2 = 4, g(4) = 4/2 = 2 f(3) = 2·3 = 6, g(6) = 6/2 = 3 f(-10) = 2·(-10) = -20, g(-20) = -20/2 = -10 Normalmente, la función inversa defse denota porf^1, pero por comodidad, ...

Asíntotas de funciones Informalmente, decimos que la función f tiene una asíntota en la recta r del plano real si la gráfica de f se acerca indefinidamente a la recta r. Ejemplo: La función f(x) = 1/x tiene asíntotas en las rectas y = 0 y x = 0: Las asíntotas pueden ser horizontales, verticales u oblicuas. La recta horizontal y = a es una asíntota horizontal de f si el límite de f(x) cuando x tiende a +infinito ó a -infinito es a. Ejemplo 1: La función exponencial f(x) = e^x tiene una ...

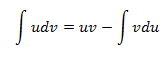
Métodos de Integración Algunas primitivas se obtienen directamente a partir de la tabla de derivadas, este es el caso de las integrales directas o inmediatas, como por ejemplo: Sin embargo, lo habitual es que resolver una integral no sea una tarea fácil, razón por la que existen distintos métodos de integración. Los métodos básicos son: integración por partes integración por sustitución integración de funciones racionales Veamos un ejemplo de cada uno de ellos: 1. Int...

Matrices y Sistemas de Ecuaciones Lineales (SEL) 1. Definición de SEL y su solución Un sistema de m ecuaciones lineales con n incógnitas (SEL) y coeficientes en un cuerpo K (como los reales o los complejos) es A los elementos ai,j se les denomina coeficientes del SEL y a los b_i términos independientes. Un ejemplo de un SEL de dos ecuaciones y dos incógnitas es Dimensión del SEL: dimensión cuadrada: si m = n (tiene el mismo número de ecuaciones que de incógnitas). dimensión...

En este artículo vamos a obtener una fórmula para calcular la derivada de una función elevada a otra función, por ejemplo: 1. La fórmula Sea la función y(x) la que queremos derivar. Supongamos que es de la forma: Es decir, la función y(x) es la función f(x) elevada a la función g(x). Para facilitar la notación, escribimos y, f y g para referirnos a las funciones y(x), f(x) y g(x), respectivamente. Las derivadas de estas funciones las escribiremos como y', f' y g'. Por tanto, la funci...

Mínim comú múltiple i màxim comú divisor 1. Descomposició de nombres Per a calcular el mínim comú múltiple o el màxim comú divisor de dos o més nombres cal descompondre aquests com un producte de potències de nombres primers. Exemple: Per descompondre un nombre dividim el nombre successivament entre nombres primers fins obtenir un 1. Més concretament: Dividim successivament per nombres primers (de manera que la divisió sigui exacta). La descomposició és el producte de les potències d...

Teorema de Pitàgores Teorema i exemples d'aplicació. 1. Teorema de Pitàgores Donat un triangle rectangle amb catets a i b i hipotenusa h (el costat oposat a l'angle recte). Aleshores, Recordem que: el triangle és rectangle perquè té un angle recte, és a dir, un angle de 90 graus ó π / 2 radiants. la hipotenusa és el costat oposat a l'angle recte Problemes d'aplicació Problema 1 Calcular la hipotenusa del triangle rectangle de costats 3cm i 4cm. Solució: Els costats só...

INTRODUCCIÓN El conocimiento de las finanzas viene siendo de gran importancia en el desarrollo personal, familiar y empresarial, lo que permite generar un proceso de mejoramiento y tranquilidad en la toma de decisiones, pero para esto es necesario entender que es lo mínimo que debemos saber y además encontrar las mejores fuentes de aprendizaje o toma de la información. A nivel organizativo y empresarial, hoy no solo las grandes empresas deben aplicar prácticas financieras, si no toda...

Os presento el proyecto colaborativo Tertulias con sabor a chocolate “una iniciativa centrada en la comunicación oral, en el diálogo, en la palabra sentida, imaginada, pensada, en la palabra que encuentra oportunidad y espacio para ser hablada y escuchada, en la palabra que, adentrándose en el universo del otro, va tejiendo respuesta...” en la que “...resuena la tradición de las comunidades de investigación fIlosófica, de las comunidades de aprendizaje, de las comunidades dialógicas” (1) Es ...

En el año 2000, Año Mundial de las Matemáticas, se instituyó la celebración del día 12 de mayo como Día Escolar de las Matemáticas por la Federación Española de Sociedades de Profesores de Matemáticas (FESPM). Esta fecha fue elegida en honor a Pedro Puig Adam, nacido el 12 de mayo de 1900 e internacionalmente reconocido en el campo de la enseñanza de las Matemáticas. Las diferentes Sociedades de Profes...

Cuando necesito algún recurso en concreto, lo busco, si lo encuentro, lo añado a mi listado particular.Lo comparto con vosotros.

Introducción Los números complejos fueron propuestos inicialmente en 1545, por el matemático italiano Girolamo Cardano, en un tratado monumental acerca de la solución de las ecuaciones cúbicas y cuarticas titulado Ars Magna. Las cantidades “ficticias” de Cardano fueron ignoradas por la mayoría de sus colegas, hasta que el genio matemático Carl Friedrich Gauss les dio el nombre actual y las utilizo para demostrar el teorema fundamental del algebra, el cual establece que todo polinomio que no ...

1.Título del proyecto: El Greco entre la Tierra y el Cielo 2. URL del proyecto: https://procomun.educalab.es/es/articulos/trabajo-final-abp-el-greco-entre-la-tierra-y-el-cielo 3. Ideas a destacar: Me ha gustado mucho la idea de crear una app a través de la cual se puedan ver las distintas obras del Greco. Es una formar original de acercar la Historia del Arte a los jóvenes utilizando simplemente sus teléfonos.También me ha gustado mucho la forma en la organiza el proyecto destacando la ev...