PROCOMÚN
Mostrando resultados 1 a 11 de un total de 11
-
Investigación sobre Pitágoras
 Actividad de investigación sobre Pitágoras, su teorema y sus aplicaciones en la vida cotidiana.Área de conocimientoContexto educativoTipo de recurso
Actividad de investigación sobre Pitágoras, su teorema y sus aplicaciones en la vida cotidiana.Área de conocimientoContexto educativoTipo de recurso -
Investigación sobre Pitágoras
 Actividad de investigación sobre Pitágoras, su teorema y sus aplicaciones en la vida cotidiana.Área de conocimientoContexto educativoTipo de recurso
Actividad de investigación sobre Pitágoras, su teorema y sus aplicaciones en la vida cotidiana.Área de conocimientoContexto educativoTipo de recurso -
Explorando los triángulos
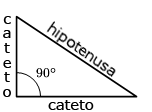 Lección sobre el uso del teorema de Pitágoras para la medición de diferentes objetos.Área de conocimientoContexto educativoTipo de recurso
Lección sobre el uso del teorema de Pitágoras para la medición de diferentes objetos.Área de conocimientoContexto educativoTipo de recurso -
REA: Teorema de Pitágoras
El REA que he escogido para esta actividad lo he localizado en Procomún, se titula:"Pythagorean Theorem". Está correctamente estructurado y organizado contando con:objetivos, contenidos, indicadores competenciales, secuencia de actividades, criterios de evaluación. Además está en inglés, lo cual, para un profesor de matemáticas bilingüe resulta del mayor interés. Se puede llevar fácilmente al aula, pues cuenta con una buena variedad de recursos: vídeo, actividades interactivas, en papel, d...Área de conocimientoContexto educativo -
Teorema del seno
 Teorema del seno El teorema del seno (o teorema de los senos) es un resultado de trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los senos de sus ángulos interiores opuestos. Esta relación fue descubierta en el siglo X. Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente). Entonces, se cumple la relación Consecuencia: Si ...Área de conocimientoContexto educativo
Teorema del seno El teorema del seno (o teorema de los senos) es un resultado de trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los senos de sus ángulos interiores opuestos. Esta relación fue descubierta en el siglo X. Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente). Entonces, se cumple la relación Consecuencia: Si ...Área de conocimientoContexto educativo -
Teorema del coseno
 Teorema del coseno El teorema del coseno (o teorema de los cosenos) es un resultado de trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los cosenos de sus ángulos interiores opuestos. Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente). Entonces, se cumplen las relaciones Nota: se dice que es una generalización de Pitágora...Área de conocimientoContexto educativo
Teorema del coseno El teorema del coseno (o teorema de los cosenos) es un resultado de trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los cosenos de sus ángulos interiores opuestos. Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente). Entonces, se cumplen las relaciones Nota: se dice que es una generalización de Pitágora...Área de conocimientoContexto educativo -
Teorema de Pitàgores (teorema i aplicació)
 Teorema de Pitàgores Teorema i exemples d'aplicació. 1. Teorema de Pitàgores Donat un triangle rectangle amb catets a i b i hipotenusa h (el costat oposat a l'angle recte). Aleshores, Recordem que: el triangle és rectangle perquè té un angle recte, és a dir, un angle de 90 graus ó π / 2 radiants. la hipotenusa és el costat oposat a l'angle recte Problemes d'aplicació Problema 1 Calcular la hipotenusa del triangle rectangle de costats 3cm i 4cm. Solució: Els costats só...Área de conocimientoContexto educativo
Teorema de Pitàgores Teorema i exemples d'aplicació. 1. Teorema de Pitàgores Donat un triangle rectangle amb catets a i b i hipotenusa h (el costat oposat a l'angle recte). Aleshores, Recordem que: el triangle és rectangle perquè té un angle recte, és a dir, un angle de 90 graus ó π / 2 radiants. la hipotenusa és el costat oposat a l'angle recte Problemes d'aplicació Problema 1 Calcular la hipotenusa del triangle rectangle de costats 3cm i 4cm. Solució: Els costats só...Área de conocimientoContexto educativo- Educación Secundaria Obligatoria
- 12 - 13 años / Primer curso
- 13 - 14 años / Segundo curso
- 14 - 15 años / Tercer curso
- 15 - 16 / Cuarto curso
- Formación Profesional
- Formación Profesional Básica (más de 15 años)
- Ciclo formativo grado medio (más de 16 años)
- Ciclo formativo grado superior (más de 18 años)
- Educación de Personas Adultas
-
Teorema de Pitágoras: Aplicaciones
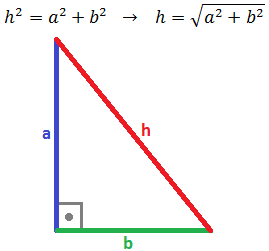 1. El teorema de Pitágoras Dado un triángulo rectángulo de catetosaybe hipotenusah(el lado opuesto al ángulo recto). Entonces, Recordemos que: el triángulo esrectánguloporque tiene un ángulo recto, es decir, un ángulo de 90 grados ó π / 2 radianes. lahipotenusaes el lado opuesto al ángulo recto Nota:hsiempre es mayor que los dos catetos, es decir,h > ayh > b. El teorema de Pitágoras es uno de los resultados más conocidos de las matemáticas y también uno de los más antiguos....Área de conocimiento
1. El teorema de Pitágoras Dado un triángulo rectángulo de catetosaybe hipotenusah(el lado opuesto al ángulo recto). Entonces, Recordemos que: el triángulo esrectánguloporque tiene un ángulo recto, es decir, un ángulo de 90 grados ó π / 2 radianes. lahipotenusaes el lado opuesto al ángulo recto Nota:hsiempre es mayor que los dos catetos, es decir,h > ayh > b. El teorema de Pitágoras es uno de los resultados más conocidos de las matemáticas y también uno de los más antiguos....Área de conocimiento -
Pitágoras muchos más que un teorema
 Primer capítulo de la serie documental Universo Matemático (http://www.rtve.es/aventura/universo-matematico) con fichas didácticas y actividades complementarias.Área de conocimiento
Primer capítulo de la serie documental Universo Matemático (http://www.rtve.es/aventura/universo-matematico) con fichas didácticas y actividades complementarias.Área de conocimiento -
Cuatro demostraciones animadas del teorema de Pitágoras
 En esta colección de escenas-animaciones se exponen cuatro demostraciones gráficas del Teorema de Pitágoras que facilitan extraordinariamente la comprensión intuitiva y formal del Teorema.Área de conocimientoContexto educativoTipo de recursoColecciones
En esta colección de escenas-animaciones se exponen cuatro demostraciones gráficas del Teorema de Pitágoras que facilitan extraordinariamente la comprensión intuitiva y formal del Teorema.Área de conocimientoContexto educativoTipo de recursoColecciones -
Teorema de Pitágoras
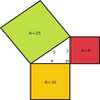 Ilustración del Teorema de Pitágoras mediante las figuras geométricas de tres cuadrados con sus áreas, cada uno de ellos compartiendo uno de los lados con los de un triángulo rectánguloTipo de recurso
Ilustración del Teorema de Pitágoras mediante las figuras geométricas de tres cuadrados con sus áreas, cada uno de ellos compartiendo uno de los lados con los de un triángulo rectánguloTipo de recurso


