La importancia de las funciones en la vida real es algo incuestionable hoy día. Su aparición en diversos campos de las ciencias, economía, sociología… es constante. Sin embargo, este uso permanente no se traduce en un protagonismo de quién realmente es el artífice de su profusa utilización: las Matemáticas. Por otro lado, el estudio de las funciones desde el punto de vista del alumnado suele resultar complejo, no sólo por la diversidad de formas en las que estas pueden presentarse sino, tam...

Tema "Límites y Continuidad" Matemáticas I 1º Bachillerato

Se hace un recorrido por ejes de coordenadas, definición de función, función continua, función discreta, máximos, mínimos, puntos de corte y periodicidad.

Curso: 2º Enseñanza: Bachillerato Nombre asignatura/materia: Matemáticas II Tipo tarea: Individual Descripción: Aplicarás el conocimiento adquirido sobre límites al estudio de un sistema de tarificación del consumo de agua.

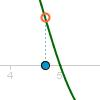
La hipótesis de este teorema es que contamos con una función F que es continua en un intervalo cerrado [a,b] cuyos valores en sus extremos F(a) y F(b) tienen distinto signo. La tesis del teorema es que, en tal caso, la función se anula en algún punto del intervalo (a,b). Esta actividad trata sobre el tema.

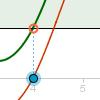
La hipótesis de este teorema es que contamos con una función F que es continua en un intervalo cerrado [a,b]. La tesis afirma que, en tal caso, la función alcanzará cualquier valor intermedio, comprendido entre F(a) y F(b). Esta actividad trata sobre el tema.

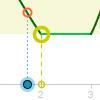
La hipótesis de este teorema es que contamos con una función F que es continua en un intervalo cerrado [a,b]. La tesis afirma que, en tal caso, existe al menos un máximo y un mínimo absolutos que la función alcanza en [a,b]. Esta actividad trata sobre el tema.