Ternas pitagóricas

Ode navigation

Hide navigation
View in full screen


Loading viewer.. Loading viewer..


Loading viewer.. Loading content..
343 Bisitak
Jarri zure webgunean

Jarri zure webgunean

INTEF

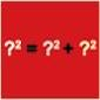
A la hora de explicar el Teorema de Pitágoras, todos conocemos muy bien el triángulo rectángulo cuyos lados miden 3, 4 y 5 o cualquier triángulo cuyos lados sen múltiplos del anterior. Posiblemente también conozcamos el que tiene por lados 5, 12 y 13. Pero, ¿existen más triángulos rectángulos cuyos lados sean números naturales? ¿Cuántos hay? En esta página se puede ver un procedimiento para obtener ternas pitagóricas.

Ezagutza arloa
Hezkuntza testuingurua
Resource type
Bildumak
Lizentzia mota Licencia de Creative Commons
Lan hau lizentziapean dago" Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
End user learner
Ekarpenak
publisher INTEF 11/01/2026 publisher INTEF . 11/01/2026 publisher INTEF 11/01/2026 author Luis Barrios Calmaestra 11/01/2026 publisher Instituto de Tecnologías Educativas (ITE) 11/01/2026 editor Instituto de Tecnologías Educativas (ITE) 11/01/2026 technical validator Andrés Piñón Fernández 11/01/2026