Unidad didáctica sobre las Gimnospermas Biología y Geología 1º ESO 12-13 añosUnidad didáctica sobre las Gimnospermas

Proyecto gamificado de animación a la lectura, basado en las tertulias dialógicas literarias. Tercer ciclo de E. Primaria.

Diseña tu campamento lunar con Tinkercad e Inteligencia Artificial.

Actividad interactiva que tiene como objetivo principal que el estudiante sea capaz de conocer las recomendaciones sobre la elección de contraseñas, desarrollando buenas prácticas a la hora de emplearlas, basándonos en las recomendaciones de la empresa líder en ciberseguridad ‘AO Kaspersky Lab.’, famosa por desarrollar el conocido antivirus ‘Kaspersky anti-virus’, que suele distribuirse como parte de la suite de programas ‘Kaspersky Internet Security’.

El uso de las TRICs (Tecnologías de la Relación, Información y la Comunicación) lleva años en una espiral de crecimiento exponencial, y un indebido uso de estas herramientas, el grado de privacidad o anonimato que ofrecen, la disminución de sensibilidad al no confrontar a la persona con la que se realiza la comunicación, puede significar, que en ocasiones, la forma de comportarse no sea la adecuada, y se esté realizando un acto de ciberacoso o de ciberbullying.

Activitat animals

En este manual se recogen tutoriales elaborados por los autores con el fin de guiar la integración de las TIC en el Aula como fuente de creatividad y de creación de situaciones de aprendizaje. Todas las herramientas utilizadas son gratuitas o bien tiene una licencia de uso gratuita con funcionalidades suficientes para su uso en el aula.

Presentación que sirve para apoyo al debate y la reflexión sobre la cuestión de las relaciones entre lenguaje y pensamiento. Lo usé con alumnos de altas capacidades de 1ºESO.

El caso práctico planteado tiene como finalidad diseñar una Base de Datos, teniendo en cuenta las necesidades planteadas en el supuesto.

Cómo diseñar pautas de trabajo cooperativo dirigida al profesorado de FP con el objeto de crear tareas consensuadas para ciclos a distancia.

La siguiente experiencia que presentamos parte de una problemática que surge en el aula a causa de las restricciones establecidas condicionadas por la situación de pandemia. Las TIC (tablets y cámara 360º) se convierten en la herramienta clave para paliar los efectos de la pandemia en las actuaciones educativas que año tras año veníamos realizando. En este caso es la docente quien expone la problemática al alumnado, y son estos quien sugieren diferentes propuestas para solucionarla, una de la...

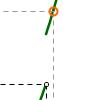
En esta actividad veremos qué significado tiene el límite por la derecha de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.

En esta actividad mediante el juego del billar se practican diversos ejemplos de simetrías axiales.

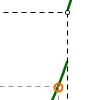
En esta actividad veremos qué significado tiene el límite por la izquierda de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.

El objetivo en esta actividad es averiguar cómo se forman figuras complejas alterando algunos elementos de figuras sencillas, como polígonos regulares y circunferencias.

En esta actividad se practica con simetrías rotacionales. Decimos que una figura plana tiene simetría rotacional cuando podemos encontrar un centro (llamado centro de rotación) de manera que si giramos la figura completa un cierto ángulo (mayor o igual a 0º y menor que 360º), la figura rotada coincide con la figura original. Cuando un figura tiene simetría rotacional, a cada punto le corresponden otro punto (que se llama "punto rotado" o "imagen") a la misma distancia del centro, de forma que...

Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta actividad podrás comprobar cómo con la simple observación directa, sin sofisticados instrumentos, Aristarco consiguió medir el tamaño aparente de la Luna y Sol en el cielo, es decir, determinar el valor del ángulo con el que los vemos.

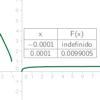
La forma más sencilla de averiguar aproximadamente a qué valor se aproxima una función F cuando x se acerca a un valor determinado c, consiste simplemente en averiguar el valor de la función para valores muy próximos a c, como F(c + 0.0001) o como F(c - 0.0001). Pero a veces el cálculo del límite es solo una operación intermedia, por lo que necesitamos valores exactos, no aproximados. Esta actividad es una herramienta útil para el cálculo de límites de funciones.

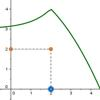
En esta actividad veremos qué significado tiene el límite de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.

Se trata de utilizar una construcción de Geogebra en la que aparecen figuras reales, piñas y girasoles, y sobre ellas se dibujan espirales y se cuenta el número de espirales en uno u otro sentido, observando que coincide siempre con dos términos consecutivos de la sucesión de Fibonacci.