PROCOMÚN
Mostrando resultados 1 a 19 de un total de 19
-
DISPENSACIÓN EN LA OFICINA DE FARMACIA
 1. La dispensación en las OF. 2. Documentos de prescripción y dispensación en OF. 3. La receta oficial del Sistema Nacional de Salud. 4. Procesos de dispensación en OF. 5. La dispensación de medicamentos con control específico. 6. Dispensación sin prescripción médica.Área de conocimientoContexto educativoTipo de recurso
1. La dispensación en las OF. 2. Documentos de prescripción y dispensación en OF. 3. La receta oficial del Sistema Nacional de Salud. 4. Procesos de dispensación en OF. 5. La dispensación de medicamentos con control específico. 6. Dispensación sin prescripción médica.Área de conocimientoContexto educativoTipo de recurso -
Derivada de una función elevada a otra
 En este artículo vamos a obtener una fórmula para calcular la derivada de una función elevada a otra función, por ejemplo: 1. La fórmula Sea la función y(x) la que queremos derivar. Supongamos que es de la forma: Es decir, la función y(x) es la función f(x) elevada a la función g(x). Para facilitar la notación, escribimos y, f y g para referirnos a las funciones y(x), f(x) y g(x), respectivamente. Las derivadas de estas funciones las escribiremos como y', f' y g'. Por tanto, la funci...Área de conocimiento
En este artículo vamos a obtener una fórmula para calcular la derivada de una función elevada a otra función, por ejemplo: 1. La fórmula Sea la función y(x) la que queremos derivar. Supongamos que es de la forma: Es decir, la función y(x) es la función f(x) elevada a la función g(x). Para facilitar la notación, escribimos y, f y g para referirnos a las funciones y(x), f(x) y g(x), respectivamente. Las derivadas de estas funciones las escribiremos como y', f' y g'. Por tanto, la funci...Área de conocimiento -
(Ecuaciones) - Ecuaciones de 2º Grado - Demostración de la Fórmula
 Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas. VÍDEOS RELACIONADOS: - Tutoriales de Ecuaciones: http://www.youtube.com/playlist?list=PLZNmE9BEzVInJZxxpaxecd3SH4TK5eggR&feature=view_all Si después de ver el vídeo te queda alguna duda del mismo, déjamelo en un comentario del vídeo e intentaré ayudarte lo antes posible. Si lo que quieres es proponerme algún tema para ...Área de conocimientoContexto educativo
Tutorial en el que se demuestra la fórmula que se utiliza para resolver las ecuaciones de 2º grado completas. VÍDEOS RELACIONADOS: - Tutoriales de Ecuaciones: http://www.youtube.com/playlist?list=PLZNmE9BEzVInJZxxpaxecd3SH4TK5eggR&feature=view_all Si después de ver el vídeo te queda alguna duda del mismo, déjamelo en un comentario del vídeo e intentaré ayudarte lo antes posible. Si lo que quieres es proponerme algún tema para ...Área de conocimientoContexto educativo -
(Funciones) - Dominio e Imagen (Fórmula): Funciones con Radicales (3)
 Tercer tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con radicales. - Inicio a 02:15: Introducción general. Funciones "buenas" y "no tan buenas". - 02:15 a 11:50: Ejemplos básicos f(x)=r2(x) y f(x)=r3(x). (Raíz cuadrada y cúbica) - 11:50 a 17:15: Ejemplo f(x)=r2(2-x). Justificación del método para el cálculo de la imagen. ...Área de conocimientoContexto educativo
Tercer tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con radicales. - Inicio a 02:15: Introducción general. Funciones "buenas" y "no tan buenas". - 02:15 a 11:50: Ejemplos básicos f(x)=r2(x) y f(x)=r3(x). (Raíz cuadrada y cúbica) - 11:50 a 17:15: Ejemplo f(x)=r2(2-x). Justificación del método para el cálculo de la imagen. ...Área de conocimientoContexto educativo -
(Ecuaciones) - Ecuaciones de 2º Grado con fórmula
 Tutorial en el que se explica la resolución de ecuaciones de 2º grado aplicando la fórmula general de resolución. VÍDEOS RELACIONADOS: - Tutoriales de Ecuaciones: http://www.youtube.com/playlist?list=PLZNmE9BEzVInJZxxpaxecd3SH4TK5eggR&feature=view_all - Demostración de la Fórmula de 2º grado: http://youtu.be/H0eJ4VXS1VQ Si después de ver el vídeo te queda alguna duda del mismo, déjamelo en un comentario del v&iacut...Área de conocimiento
Tutorial en el que se explica la resolución de ecuaciones de 2º grado aplicando la fórmula general de resolución. VÍDEOS RELACIONADOS: - Tutoriales de Ecuaciones: http://www.youtube.com/playlist?list=PLZNmE9BEzVInJZxxpaxecd3SH4TK5eggR&feature=view_all - Demostración de la Fórmula de 2º grado: http://youtu.be/H0eJ4VXS1VQ Si después de ver el vídeo te queda alguna duda del mismo, déjamelo en un comentario del v&iacut...Área de conocimiento -
(Funciones) - Dominio e Imagen (Fórmula): Funciones Polinómicas (1)
 Primer tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones polinómicas. - Inicio a 03:21: Introducción general y definiciones básicas. - 03:21 a 05:10: Ejemplo introductorio. - 05:10 a 10:00: Ejemplo de función polinómica de grado 1. - 05:10 a 24:05: Ejemplos de funciones polinómicas de grado 2. + Método de la función inversa (12:30 y 19:1...Área de conocimientoContexto educativo
Primer tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones polinómicas. - Inicio a 03:21: Introducción general y definiciones básicas. - 03:21 a 05:10: Ejemplo introductorio. - 05:10 a 10:00: Ejemplo de función polinómica de grado 1. - 05:10 a 24:05: Ejemplos de funciones polinómicas de grado 2. + Método de la función inversa (12:30 y 19:1...Área de conocimientoContexto educativo -
(Funciones) - Dominio e Imagen (Fórmula): Funciones con Quebrados (2)
 Segundo tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con quebrados algebraicos. - Inicio a 02:42: Introducción general. funciones "buenas" y "no tan buenas". - 02:42 a 08:55: Ejemplo f(x)=2/x (muy detallado). - 08:55 a 13:22: Ejemplo f(x)=-5/(x+2). - 13:22 a 15:00: Ejemplo f(x)=1/(x-3) + 2. - 15:00 a 18:03: Ejemplo f(x)=2/x^2. - 18:03 a 21:45: Ejemplo f(x)=-4/(x^...Área de conocimientoContexto educativo
Segundo tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula, en este caso de funciones con quebrados algebraicos. - Inicio a 02:42: Introducción general. funciones "buenas" y "no tan buenas". - 02:42 a 08:55: Ejemplo f(x)=2/x (muy detallado). - 08:55 a 13:22: Ejemplo f(x)=-5/(x+2). - 13:22 a 15:00: Ejemplo f(x)=1/(x-3) + 2. - 15:00 a 18:03: Ejemplo f(x)=2/x^2. - 18:03 a 21:45: Ejemplo f(x)=-4/(x^...Área de conocimientoContexto educativo -
JUMP: la fórmula para crear escuelas excelentes (y baratas) sin dejar a nadie atrás
 El dramaturgo y matemático canadienseJohn Mighton, emprendedor Ashoka y fundador delprograma JUMP("Junior Undiscovered Math Prodigies"), quetrata de implantar en las escuelas una nueva forma de enseñar matemáticas, tiene una idea clara: a muchos niños no se les da la oportunidad de mejorar sencillamente porque sus profesores no se preocupan de ayudarles. Pensamos, porque así nos lo han enseñado, que hay niños que, sencillamente, no ti...
El dramaturgo y matemático canadienseJohn Mighton, emprendedor Ashoka y fundador delprograma JUMP("Junior Undiscovered Math Prodigies"), quetrata de implantar en las escuelas una nueva forma de enseñar matemáticas, tiene una idea clara: a muchos niños no se les da la oportunidad de mejorar sencillamente porque sus profesores no se preocupan de ayudarles. Pensamos, porque así nos lo han enseñado, que hay niños que, sencillamente, no ti... -
(Funciones) - Dominio e Imagen (Fórmula) (4)
 Cuarto tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula y en este caso interviene el valor absoluto de funciones y cuando aparecen mezcladas funciones polinómicas, con quebrados y radicales. - Inicio a 01:55: Introducción general. Funciones "buenas" y "no tan buenas". - 01:55 a 04:45: Ejemplo f(x)=3. - 04:45 a 07:53: Ejemplo f(x)=|x^2+2x|. - 07:53 a 11:05: Ejemplo f(x)=|-x^2+6x-8| - 11:...Área de conocimientoContexto educativo
Cuarto tutorial en el que se explica el cálculo del dominio e imagen (recorrido) de funciones dadas por su fórmula y en este caso interviene el valor absoluto de funciones y cuando aparecen mezcladas funciones polinómicas, con quebrados y radicales. - Inicio a 01:55: Introducción general. Funciones "buenas" y "no tan buenas". - 01:55 a 04:45: Ejemplo f(x)=3. - 04:45 a 07:53: Ejemplo f(x)=|x^2+2x|. - 07:53 a 11:05: Ejemplo f(x)=|-x^2+6x-8| - 11:...Área de conocimientoContexto educativo -
Diferentes formas de expresar una función: paso de enunciado a fórmula
 En esta actividad se trabaja el paso de el enunciado a la fórmula de una funciónÁrea de conocimientoContexto educativoTipo de recurso
En esta actividad se trabaja el paso de el enunciado a la fórmula de una funciónÁrea de conocimientoContexto educativoTipo de recurso -
Derivada de una función elevada a otra función
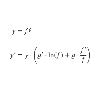 En este documento vamos a calcular una fórmula para obtener la derivada de una función elevada a otra función: y(x) = f(x)^(g(x)). Aplicaremos las propiedades de los logaritmos (logaritmo de una potencia) para evitar el exponente . Después, derivamos la igualdad obtenida (derivada del logaritmo y regla de la cadena). Finalmente, aislamos la derivada de y obteniendo una fórmula. El documento contiende dos ejemplos de aplicación de la fórmula.Área de conocimientoContexto educativoTipo de recurso
En este documento vamos a calcular una fórmula para obtener la derivada de una función elevada a otra función: y(x) = f(x)^(g(x)). Aplicaremos las propiedades de los logaritmos (logaritmo de una potencia) para evitar el exponente . Después, derivamos la igualdad obtenida (derivada del logaritmo y regla de la cadena). Finalmente, aislamos la derivada de y obteniendo una fórmula. El documento contiende dos ejemplos de aplicación de la fórmula.Área de conocimientoContexto educativoTipo de recurso -
Ecuación de dimensiones
 Concepto de ecuación de dimensiones.Área de conocimientoContexto educativoTipo de recursoColecciones
Concepto de ecuación de dimensiones.Área de conocimientoContexto educativoTipo de recursoColecciones -
Áreas de polígonos
 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Esta aplicación se compone de dos escenas, en la primera, con seis apartados, se trata de ver, moviendo los puntos, qué cosas se mantienen sin variar y qué cosas cambian al mover los puntos y de ese modo relacionar el área de un triángulo o de un trapecio con la del rectángulo. En la segunda escena se des...Área de conocimientoContexto educativoTipo de recursoColecciones
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Esta aplicación se compone de dos escenas, en la primera, con seis apartados, se trata de ver, moviendo los puntos, qué cosas se mantienen sin variar y qué cosas cambian al mover los puntos y de ese modo relacionar el área de un triángulo o de un trapecio con la del rectángulo. En la segunda escena se des...Área de conocimientoContexto educativoTipo de recursoColecciones -
Área y volumen de un prisma
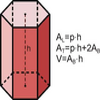 Ilustración de la figura geométrica de un prisma y de las fórmulas para hallar sus áreas lateral y total, y su volumenTipo de recurso
Ilustración de la figura geométrica de un prisma y de las fórmulas para hallar sus áreas lateral y total, y su volumenTipo de recurso -
Área y volumen de un cilindro
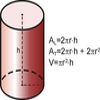 Ilustración de la figura geométrica de un cilindro y de las fórmulas para hallar sus áreas lateral y total, y su volumenTipo de recurso
Ilustración de la figura geométrica de un cilindro y de las fórmulas para hallar sus áreas lateral y total, y su volumenTipo de recurso -
Área y volumen de una pirámide
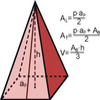 Ilustración de la figura geométrica de una pirámide y de las fórmulas para hallar sus áreas lateral y total, y su volumenTipo de recurso
Ilustración de la figura geométrica de una pirámide y de las fórmulas para hallar sus áreas lateral y total, y su volumenTipo de recurso -
Área y volumen de un cono
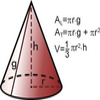 Ilustración de la figura geométrica de un cono y de las fórmulas para hallar sus áreas lateral y total, y su volumenTipo de recurso
Ilustración de la figura geométrica de un cono y de las fórmulas para hallar sus áreas lateral y total, y su volumenTipo de recurso -
Área y volumen de una esfera
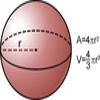 Ilustración de la figura geométrica de una esfera y de la fórmula para hallar su área y su volumenTipo de recurso
Ilustración de la figura geométrica de una esfera y de la fórmula para hallar su área y su volumenTipo de recurso -
Teorema de Pitágoras
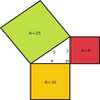 Ilustración del Teorema de Pitágoras mediante las figuras geométricas de tres cuadrados con sus áreas, cada uno de ellos compartiendo uno de los lados con los de un triángulo rectánguloTipo de recurso
Ilustración del Teorema de Pitágoras mediante las figuras geométricas de tres cuadrados con sus áreas, cada uno de ellos compartiendo uno de los lados con los de un triángulo rectánguloTipo de recurso


