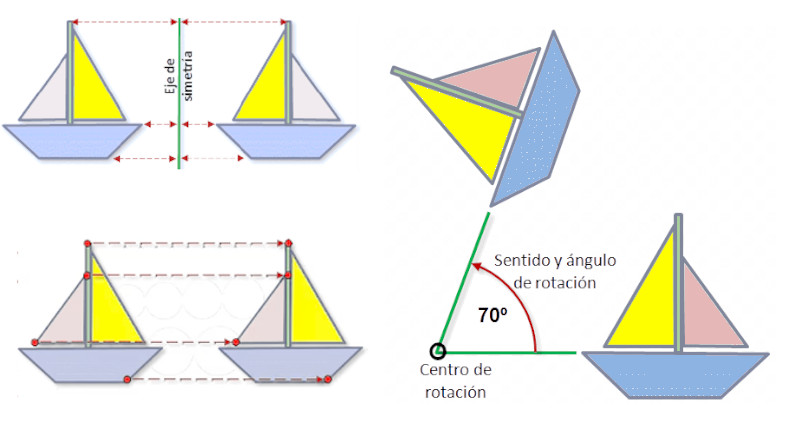Se trata de una unidad para trabajar las traslaciones, los giros y las simetrías tanto axiales como centrales. Se enmarca en la asignaturas de Matemáticas de 3º ESO (Sistema educativo español).

El título de la propuesta se basa en el grabado de M. C. Escher “Metamorphosis II” en el cual, a partir de la palabra "METAMORPHOSE", la composición de elementos geométricos básicos se va transformando en una sucesión de teselaciones cada vez más complejas y orgánicas. Esta propuesta se inspira en dicha obra ya que pretende, a partir de los movimientos básicos del plano (traslación, rotación y simetría), desarrollar un proceso de enseñanza-aprendizaje que evolucione (metamorfósis) a la obtenc...

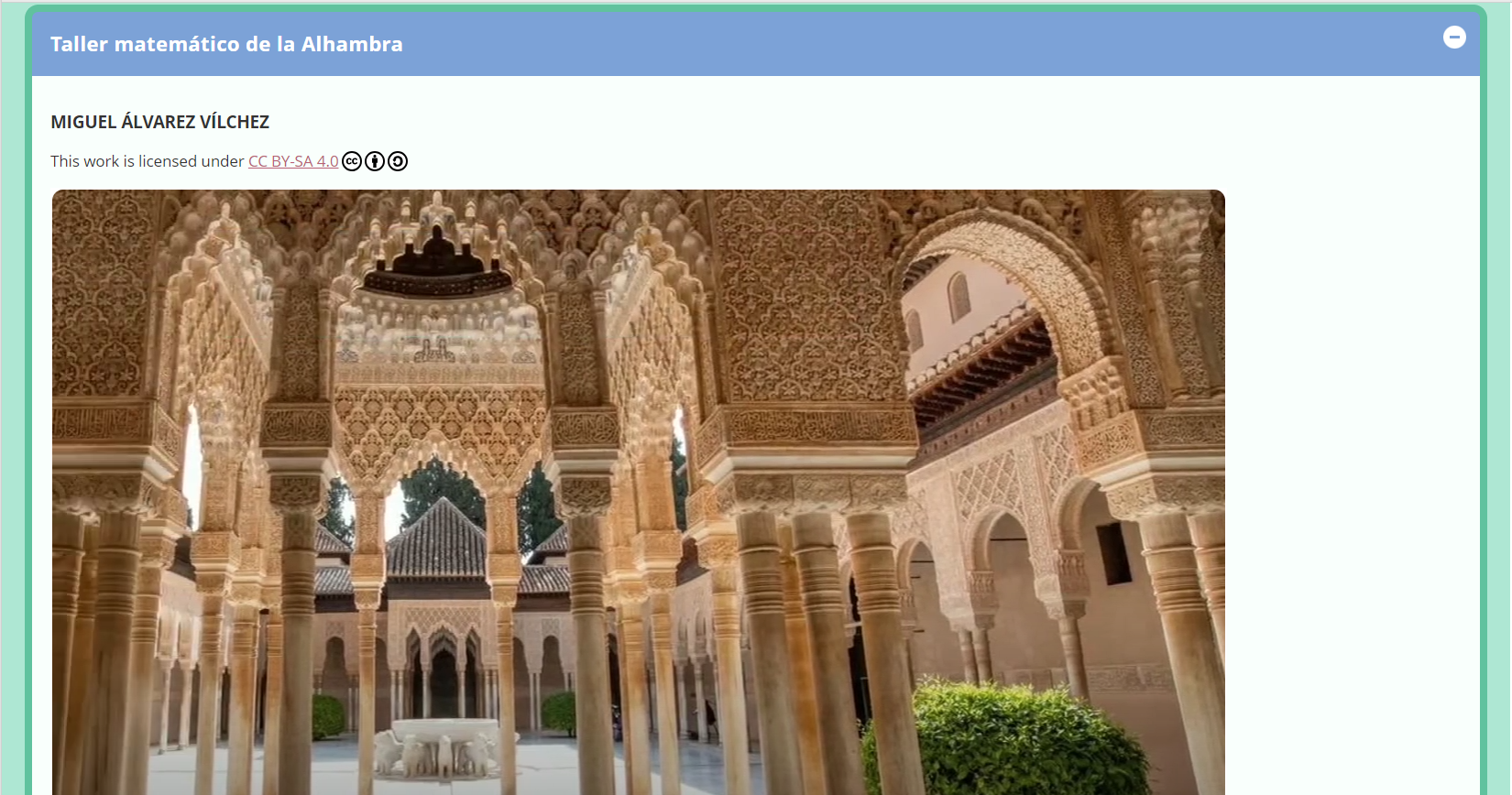Taller matemático en el que se pretende que el alumnado de primer ciclo de la ESO aprenda a desarrollar sobre las figuras geométricas de la Alhambra una cenefa bien vía digital o bien vía papel, para desarrollarlo como producto final de la situación de aprendizaje propuesta.

El objetivo de este proyecto es que los alumnos aprendan geometría, más concretamente, las distintas transformaciones geométricas en el plano (traslaciones, giros y simetrías e incluso componer estos movimientos) mediante la creación de mosaicos, frisos y rosetones utilizando para ello el entorno Scratch y además jueguen con la creatividad usando distintas figuras y formas. Aunque el proyecto está dirigido al nivel de 3º ESO en el área de Matemáticas se podría aplicar a cualquier nivel de Se...

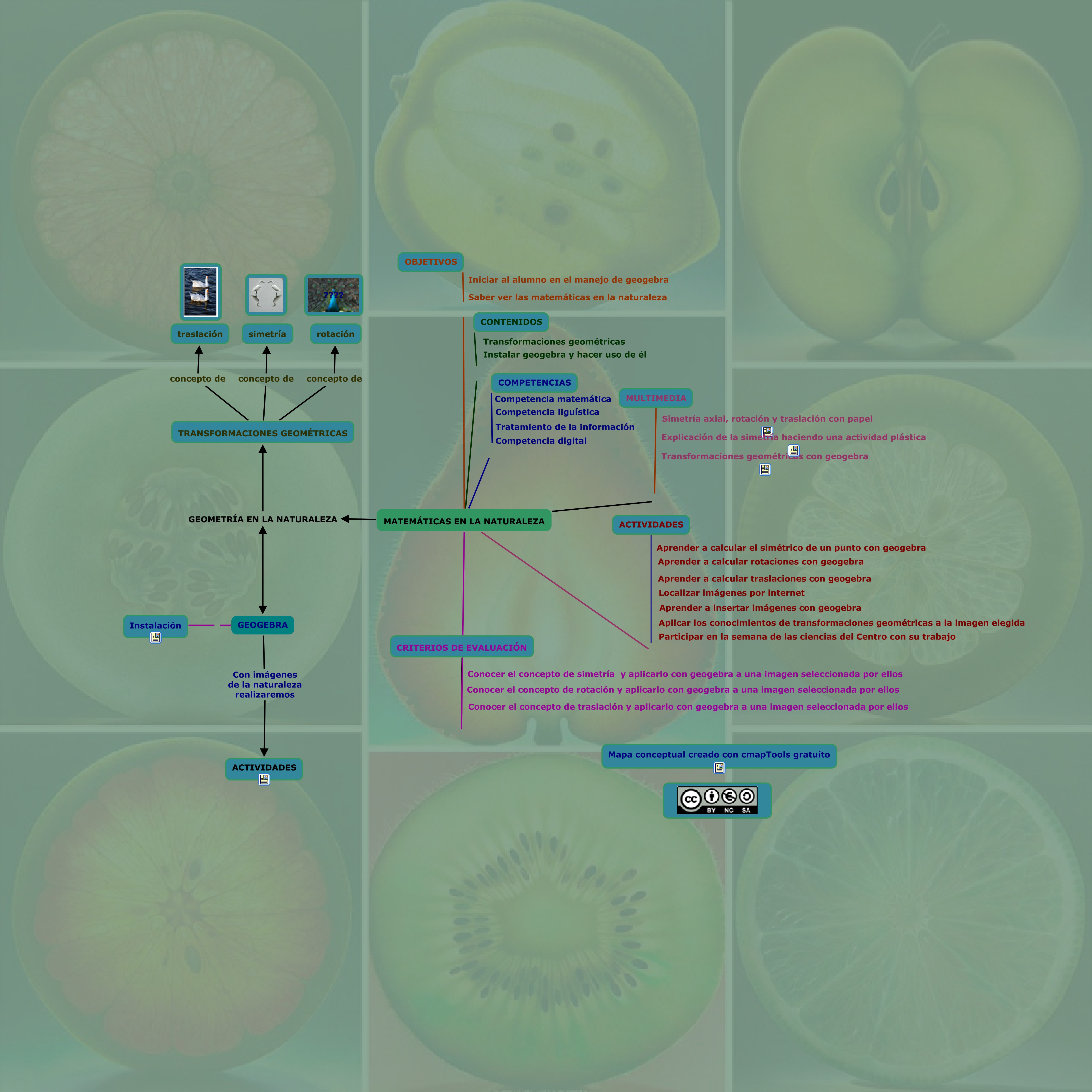Mapa conceptual referente a GEOMETRÍA EN LA NATURALEZA. Pertenece a la actividad 2.1 del curso a distancia. Dirección URL:http://cmapspublic.ihmc.us/rid=1NX8SQ70Y-R04Q3L-2HXH/geometr%C3%ADa%20en%20la%20naturaleza.cmap Ha sido creado con cmapTools, programa gratuito que podreis encontrar en http://dfiles.eu/files/6pwyooh4t

Tutorial en el que se explica como representar funciones del tipo f(x)=ax^2+bx+c utilizando la traslación de ejes. VÍDEOS RELACIONADOS: - Representación Gráfica de Funciones Parabólicas (Método General): http://www.youtube.com/watch?feature=player_embedded&v=9i7FswIaNx0 Si después de ver el vídeo te queda alguna duda del mismo, déjamelo en un comentario del vídeo e intentaré ayudarte lo antes posible. Si lo que...

Tres escenas: traslación, giro, simetría; construidas con el applet Descartes que resumen las principales transformaciones geométricas.

Dos escenas: cenefas, mosaicos; construidas con el applet Descartes que permiten observar la construcción de cenefas y mosaicos a partir de un mismo patrón.

En este trabajo se estudian de las características de las transformaciones relacionadas con las traslaciones y homotecias.

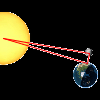Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta actividad podrás comprobar cómo se las ingenió Aristarco para calcular la distancia al Sol y su tamaño.

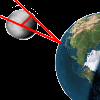Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta actividad podrás comprobar cómo mediante la observación del eclipse de Sol y el eclipse de Luna, Aristarco consiguió calcular el tamaño de la Luna y la distancia a ella.