Los vectores y las matrices aunque no representan un uso explícito común, juegan un papel crucial en las matemáticas modernas y se usan para representar informaciones, describir fenómenos de la vida cotidiana y resolver problemas de distintas áreas como la física, la informática y la ingeniería.

Tema de matrices y determinantes para Matemáticas Aplicadas a las Ciencias Sociales II

Matrices: concepto, suma, producto, transpuesta, determinante, adjunta e inversa. 1. Concepto de Matriz y operaciones básicas 1.1. Concepto Una matriz es un conjunto ordenado de números. Los números están ordenados por filas y por columnas. La dimensión de una matriz es m x n, siendo m el número de filas y n el número de columnas. Cuando m = n, se dice que la matriz es una matriz cuadrada de dimensión m. Ejemplo de una matriz: Esta matriz tiene 3 filas y 3 columnas. Por tanto, es una...

Matrices y Sistemas de Ecuaciones Lineales (SEL) 1. Definición de SEL y su solución Un sistema de m ecuaciones lineales con n incógnitas (SEL) y coeficientes en un cuerpo K (como los reales o los complejos) es A los elementos ai,j se les denomina coeficientes del SEL y a los b_i términos independientes. Un ejemplo de un SEL de dos ecuaciones y dos incógnitas es Dimensión del SEL: dimensión cuadrada: si m = n (tiene el mismo número de ecuaciones que de incógnitas). dimensión...

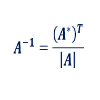En este documento definimos matriz inversa de una matriz cuadrada y proporcionamos los dos métodos básicos para calcularla: inversa por Gauss y por la matriz adjunta. Temas de matrices: Matriz adjunta Suma de matrices Multiplicar matrices (1) Multiplicar matrices (2) Eliminación de Gauss (1) Eliminación de Gauss (2) Determinantes de matrices (1) Determinantes de matrices (2) Matriz inversa (1) Matriz inversa (por Gauss) (2) Matriz inversa (por determinantes) (3) Ejemplos del teorema de Rouch...

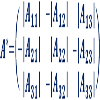En este documento vamos a explicar cómo se calcula la matriz adjunta o de cofactores de una matriz y calcularemos la matriz adjunta de 2 matrices de dimensión 2x2 y 3x3. Temas de matrices: Matriz adjunta Suma de matrices Multiplicar matrices (1) Multiplicar matrices (2) Eliminación de Gauss (1) Eliminación de Gauss (2) Determinantes de matrices (1) Determinantes de matrices (2) Matriz inversa (1) Matriz inversa (por Gauss) (2) Matriz inversa (por determinantes) (3) Ejemplos del teorema de Ro...

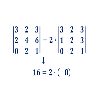En este documento enumeramos las principales propiedades de la función determinante de una matriz cuadrada, con ejemplos. Recordad que existen reglas para el cálculo del determinante (como Sarrus y Laplace), que no proporcionamos por su extensión. Temas de matrices: Suma de matrices Multiplicar matrices (1) Multiplicar matrices (2) Eliminación de Gauss (1) Eliminación de Gauss (2) Determinantes de matrices (1) Determinantes de matrices (2) Matriz inversa (1) Matriz inversa (por Gauss) (2) Ma...

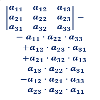En este documento explicamos cómo se calcula el determinante de una matriz cuadrada de dimensión 1, 2 y 3. También, proporcionamos la fórmula de Laplace para el cálculo de determinantes. Incluimos ejemplos y enlaces a páginas con problemas resueltos. Temas de matrices: Suma de matrices Multiplicar matrices (1) Multiplicar matrices (2) Eliminación de Gauss (1) Eliminación de Gauss (2) Determinantes de matrices (1) Determinantes de matrices (2) Matriz inversa (1) Matriz inversa (por Gauss) (2)...

En esta aplicación se puede practicar el producto de matrices y el cálculo de matrices inversas. Puede utilizarse para matrices cuadradas de orden 2 y 3.