PROCOMÚN
Mostrando resultados 1 a 19 de un total de 19
-
The city
 The aim of this interactive teaching and learning resource is to differentiate between urban spaces and their different features by reading a map. The medium used is a game in which the different areas of the city are shown and, according to the characteristics indicated, the user must point to them on the map. Aimed at students aged from 12 to 16 years. Year of creation: 2020. https://www.ign.es/recursos-educativos/descubre-territorio/ciudad.htmlÁrea de conocimientoContexto educativo
The aim of this interactive teaching and learning resource is to differentiate between urban spaces and their different features by reading a map. The medium used is a game in which the different areas of the city are shown and, according to the characteristics indicated, the user must point to them on the map. Aimed at students aged from 12 to 16 years. Year of creation: 2020. https://www.ign.es/recursos-educativos/descubre-territorio/ciudad.htmlÁrea de conocimientoContexto educativo -
La ciudad
 Este recurso interactivo y didáctico tiene como objetivo diferenciar los espacios urbanos y sus diferentes funciones mediante la lectura cartográfica. El soporte es un juego en el que se van explicando las diferentes zonas de la ciudad y el usuario, según las características indicadas, debe ir señalándolas en el mapa. Dirigido a estudiantes de edades de entre 12 y 16 años. Actualizado en 2020. También se ofrece este recurso en inglés. https://www.ign.es/recursos-educativos/descubre-...Área de conocimientoContexto educativo
Este recurso interactivo y didáctico tiene como objetivo diferenciar los espacios urbanos y sus diferentes funciones mediante la lectura cartográfica. El soporte es un juego en el que se van explicando las diferentes zonas de la ciudad y el usuario, según las características indicadas, debe ir señalándolas en el mapa. Dirigido a estudiantes de edades de entre 12 y 16 años. Actualizado en 2020. También se ofrece este recurso en inglés. https://www.ign.es/recursos-educativos/descubre-...Área de conocimientoContexto educativo -
Hexágono regular
 Hexágono regular Un hexágono regular es un hexágono cuyos lados y ángulos miden lo mismo. Los ángulos (interiores) miden 120º. Un pentágono regular tiene 9 diagonales y su área es donde l es la medida del lado y ap la del apotema (segmento que une el centro del pentágono con el punto medio de cualquiera de sus lados). Problema 1: Si el lado de un hexágono regular mide 6cm y su apotema mide 5.2cm,¿cuál es el perímetro y el área de dicho hexágono? Solución: Lo...Área de conocimiento
Hexágono regular Un hexágono regular es un hexágono cuyos lados y ángulos miden lo mismo. Los ángulos (interiores) miden 120º. Un pentágono regular tiene 9 diagonales y su área es donde l es la medida del lado y ap la del apotema (segmento que une el centro del pentágono con el punto medio de cualquiera de sus lados). Problema 1: Si el lado de un hexágono regular mide 6cm y su apotema mide 5.2cm,¿cuál es el perímetro y el área de dicho hexágono? Solución: Lo...Área de conocimiento -
Hexágono regular
 Pentágono regular Un pentágono regular es un pentágono cuyos lados y ángulos miden lo mismo. Los ángulos (interiores) miden 108º. Un pentágono regular tiene 5 diagonales y su área es donde l es la medida del lado y ap la del apotema (segmento que une el centro del pentágono con el punto medio de cualquiera de sus lados). Problema 1: Calcular el perímetro de un pentágono regular de lado 1.5cm y apotema 1.03cm: Solución: Para calcular el perímetro sólo necesit...Área de conocimiento
Pentágono regular Un pentágono regular es un pentágono cuyos lados y ángulos miden lo mismo. Los ángulos (interiores) miden 108º. Un pentágono regular tiene 5 diagonales y su área es donde l es la medida del lado y ap la del apotema (segmento que une el centro del pentágono con el punto medio de cualquiera de sus lados). Problema 1: Calcular el perímetro de un pentágono regular de lado 1.5cm y apotema 1.03cm: Solución: Para calcular el perímetro sólo necesit...Área de conocimiento -
Área de un Triángulo
 Área de un Triángulo Principalmente, hay dos formas de calcular el área de un triángulo: la mitad de la base por altura y la fórmula de Herón. El área de un triángulo de altura h y base b es la mitad del producto de la altura por la la base: área = b·h/2 Ejemplo: el triángulo equilátero (todos los lados miden lo mismo) de lado 3cm (y, por tanto, altura 2,6cm) tiene área Una demostración intuitiva de esta fórmula consiste en cortar el triángulo para formar un cuadrado: áreas de tri...Área de conocimiento
Área de un Triángulo Principalmente, hay dos formas de calcular el área de un triángulo: la mitad de la base por altura y la fórmula de Herón. El área de un triángulo de altura h y base b es la mitad del producto de la altura por la la base: área = b·h/2 Ejemplo: el triángulo equilátero (todos los lados miden lo mismo) de lado 3cm (y, por tanto, altura 2,6cm) tiene área Una demostración intuitiva de esta fórmula consiste en cortar el triángulo para formar un cuadrado: áreas de tri...Área de conocimiento -
Analisis REA: "El área de las figuras planas"
El recurso seleccionado para elaborar el análisis lleva por título "El área de las figuras planas". Podréis visitarlo a través del siguiente enlace:http://procomun.educalab.es/es/ode/view/1445270077894 El recurso trata de esclarecer el origen de las fórmulas utilizadas para el cálculo de algunas áreas de figuras planas. En cuanto a la organización del recurso, está subdividida en apartados, que estructuran de manera muy clara el recurso, y ayudan a su seguimiento y desarrollo. Así mismo ci...Área de conocimientoContexto educativo -
Distintas áreas en una misma competencia educativa #STEMooc
A continuación os detallo sendos enlaces relativos al enunciado del Post: http://www.joanteixido.org/doc/CB/nuevo-enfoque.pdf http://www.adide.org/revista/index.php?option=com_content&task=view&id=467&Itemid=72 Ambos contenidos resultan enriquecedores y nos llevan a una visión más global de la concepción actual de la educación basada en la adquisición de comptencias. No obstante, me gustaría hacer hincapié en el segundo de los links. "EL VALOR DE LAS DIFERENTES ÁREAS EN LA EVA...Área de conocimientoContexto educativo -
Cálculo de áreas de regiones sombreadas
 El cálculo de áreas de figuras geométricas se hace útil cuando debemos determinar el área de una región no convencional; es decir, regiones cuya forma no es geométricamente tradicional como los cuadrilateros, triángulos, círculos y polígonos en general. En esta unidad se presentan algunas regiones no convencionales para el cálculo de su área. Igualmente se suministran las ayudas necesarias en caso de no conocerse el procedimiento adecuado para dicho cálculo. CÁLCULO DE ÁREAS DE REGIONES SOM...Área de conocimientoContexto educativo
El cálculo de áreas de figuras geométricas se hace útil cuando debemos determinar el área de una región no convencional; es decir, regiones cuya forma no es geométricamente tradicional como los cuadrilateros, triángulos, círculos y polígonos en general. En esta unidad se presentan algunas regiones no convencionales para el cálculo de su área. Igualmente se suministran las ayudas necesarias en caso de no conocerse el procedimiento adecuado para dicho cálculo. CÁLCULO DE ÁREAS DE REGIONES SOM...Área de conocimientoContexto educativo -
Cuerpos de revolución
 Estas actividades están preparadas para verse en pantalla de 17 pulgadas y con una resolución de 1024 por 768 pixeles, ya que en algunas escenas aparecen mediciones en centímetros y milímetros que en caso de verse con otra configuración su tamaño no se corresponderá con lo real, incluso puede ser que el tamaño de algunas escenas sea demasiado grande. También se necesitará papel y lápiz para hacer los cálculos y las deducciones de las ecuaciones que se piden en estas actividades. Tras estos ej...Área de conocimientoContexto educativoTipo de recursoColecciones
Estas actividades están preparadas para verse en pantalla de 17 pulgadas y con una resolución de 1024 por 768 pixeles, ya que en algunas escenas aparecen mediciones en centímetros y milímetros que en caso de verse con otra configuración su tamaño no se corresponderá con lo real, incluso puede ser que el tamaño de algunas escenas sea demasiado grande. También se necesitará papel y lápiz para hacer los cálculos y las deducciones de las ecuaciones que se piden en estas actividades. Tras estos ej...Área de conocimientoContexto educativoTipo de recursoColecciones -
El área de un triángulo
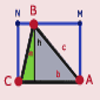 Comprobación dinámica de la fórmula del área de un triángulo.Área de conocimientoContexto educativoTipo de recursoColecciones
Comprobación dinámica de la fórmula del área de un triángulo.Área de conocimientoContexto educativoTipo de recursoColecciones -
Justificación geométrica del producto de la suma de dos números por su diferencia
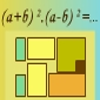 Justificación geométrica del producto de un binomio suma por un binomio diferencia apoyada por cinco ejercicios relativos a la misma.Área de conocimientoContexto educativoTipo de recursoColecciones
Justificación geométrica del producto de un binomio suma por un binomio diferencia apoyada por cinco ejercicios relativos a la misma.Área de conocimientoContexto educativoTipo de recursoColecciones -
Justificación geométrica del cuadrado de la diferencia de dos números
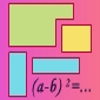 Justificación geométrica del cuadrado de la diferencia de dos números apoyada por cinco ejercicios relativos a la misma.Área de conocimientoContexto educativoTipo de recursoColecciones
Justificación geométrica del cuadrado de la diferencia de dos números apoyada por cinco ejercicios relativos a la misma.Área de conocimientoContexto educativoTipo de recursoColecciones -
Construir triángulos de área dada
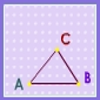 Construcción de triángulos con ayuda del geoplano virtual.Área de conocimientoContexto educativoTipo de recursoColecciones
Construcción de triángulos con ayuda del geoplano virtual.Área de conocimientoContexto educativoTipo de recursoColecciones -
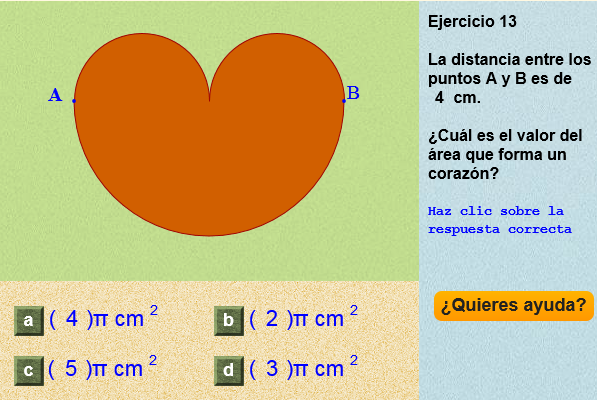
Corazón partío
 Este es un objeto educativo del Proyecto Gauss, desarrollado por el INTEF para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Esta actividad es un ejemplo práctico del teorema fundamental del cálculo integral.Área de conocimientoContexto educativoTipo de recursoColecciones
Este es un objeto educativo del Proyecto Gauss, desarrollado por el INTEF para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Esta actividad es un ejemplo práctico del teorema fundamental del cálculo integral.Área de conocimientoContexto educativoTipo de recursoColecciones -
Corona
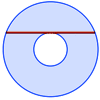 Utilizando Geogebra, se realiza una construcción para relacionar el teorema de Pitágoras con el área de una corona circular.Área de conocimientoContexto educativoTipo de recursoColecciones
Utilizando Geogebra, se realiza una construcción para relacionar el teorema de Pitágoras con el área de una corona circular.Área de conocimientoContexto educativoTipo de recursoColecciones -
Áreas de polígonos
 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Esta aplicación se compone de dos escenas, en la primera, con seis apartados, se trata de ver, moviendo los puntos, qué cosas se mantienen sin variar y qué cosas cambian al mover los puntos y de ese modo relacionar el área de un triángulo o de un trapecio con la del rectángulo. En la segunda escena se des...Área de conocimientoContexto educativoTipo de recursoColecciones
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Esta aplicación se compone de dos escenas, en la primera, con seis apartados, se trata de ver, moviendo los puntos, qué cosas se mantienen sin variar y qué cosas cambian al mover los puntos y de ese modo relacionar el área de un triángulo o de un trapecio con la del rectángulo. En la segunda escena se des...Área de conocimientoContexto educativoTipo de recursoColecciones -
Perímetro
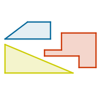 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta aplicación repasaremos el concepto de perímetro y su posible relación o no con el área.Área de conocimientoContexto educativoTipo de recursoColecciones
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta aplicación repasaremos el concepto de perímetro y su posible relación o no con el área.Área de conocimientoContexto educativoTipo de recursoColecciones -
Áreas en el geoplano
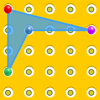 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta aplicación vamos a hallar áreas de diferentes polígonos utilizando una cuadrícula o un geoplano (una malla cuadrada de puntos); para la medida de las áreas ten en cuenta que la cuadrícula del geoplano está formada por cuadraditos de 1 cm de lado.Área de conocimientoContexto educativoTipo de recursoColecciones
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta aplicación vamos a hallar áreas de diferentes polígonos utilizando una cuadrícula o un geoplano (una malla cuadrada de puntos); para la medida de las áreas ten en cuenta que la cuadrícula del geoplano está formada por cuadraditos de 1 cm de lado.Área de conocimientoContexto educativoTipo de recursoColecciones -
El área de las figuras planas
 Este Recurso Educativo Abierto ha sido diseñado para su integración dentro de una Unidad Didáctica sobre "El área de las figuras planas" que se imparte dentro del bloque de Geometría de las Matemáticas de 1º de ESO. Está formado fundamentalmente por applets dinámicos de GeoGebra, vídeos y cuestiones para potenciar la reflexión, de modo que el alumno sea capaz de sacar sus propias conclusiones, y construir así su aprendizaje.Área de conocimientoContexto educativoTipo de recurso
Este Recurso Educativo Abierto ha sido diseñado para su integración dentro de una Unidad Didáctica sobre "El área de las figuras planas" que se imparte dentro del bloque de Geometría de las Matemáticas de 1º de ESO. Está formado fundamentalmente por applets dinámicos de GeoGebra, vídeos y cuestiones para potenciar la reflexión, de modo que el alumno sea capaz de sacar sus propias conclusiones, y construir así su aprendizaje.Área de conocimientoContexto educativoTipo de recurso


