PROCOMÚN
Mostrando resultados 1141 a 1160 de un total de 1796
-
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
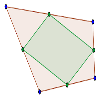 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
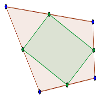 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
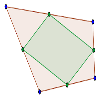 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
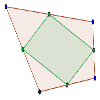 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
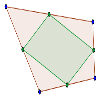 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
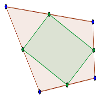 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
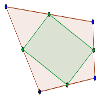 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
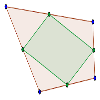 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Los puntos medios de los lados de un cuadrilátero forman un paralelogramo.
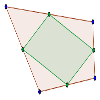 Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso
Demostrar que en cualquier cuadrilátero, los puntos medios de sus cuatro lados son los vértices de un paralelogramo interior al cuadrilátero.Área de conocimientoContexto educativoTipo de recurso -
Paralelogramo
 Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso
Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso -
Paralelogramo
 Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso
Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso -
Paralelogramo
 Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso
Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso -
Paralelogramo
 Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso
Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso -
Paralelogramo
 Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso
Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramo.Área de conocimientoContexto educativoTipo de recurso -
eXe_paralelogramo
 Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramoÁrea de conocimientoContexto educativoTipo de recurso
Demostración de que los puntos centrales de cualquier cuadrilátero forman un paralelogramoÁrea de conocimientoContexto educativoTipo de recurso -
Polígono de cuatro lados. Paralelogramo.
 En la actividad se construye a partir de un polígono de cuatro lados un paralelogramo. Se comprueba gráfica y empíricamente (Tales) que lo es.Área de conocimientoContexto educativoTipo de recurso
En la actividad se construye a partir de un polígono de cuatro lados un paralelogramo. Se comprueba gráfica y empíricamente (Tales) que lo es.Área de conocimientoContexto educativoTipo de recurso -
Polígono de cuatro lados. Paralelogramo.
 En la actividad se construye a partir de un polígono de cuatro lados un paralelogramo. Se comprueba gráfica y empíricamente (Tales) que lo es.Área de conocimientoContexto educativoTipo de recurso
En la actividad se construye a partir de un polígono de cuatro lados un paralelogramo. Se comprueba gráfica y empíricamente (Tales) que lo es.Área de conocimientoContexto educativoTipo de recurso -
Polinomios de Taylor
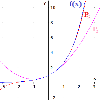 En este documento definimos el polinomio de Taylor de una función de una variable y enunciamos el teorema de la fórmula de Taylor con resto de Lagrange. También, calculamos los polinomios de grado 2 y grado 5 de la función exponencial y proporcionamos las cotas del error obtenido en la aproximación para el intervalo _0,1_. Recursos de Cálculo Diferencial: Teorema de Taylor con resto de Lagrange Introducción al Cálculo Diferencial (teoría) Tabla de derivadas elementales y reglas de derivación...Área de conocimientoContexto educativoTipo de recurso
En este documento definimos el polinomio de Taylor de una función de una variable y enunciamos el teorema de la fórmula de Taylor con resto de Lagrange. También, calculamos los polinomios de grado 2 y grado 5 de la función exponencial y proporcionamos las cotas del error obtenido en la aproximación para el intervalo _0,1_. Recursos de Cálculo Diferencial: Teorema de Taylor con resto de Lagrange Introducción al Cálculo Diferencial (teoría) Tabla de derivadas elementales y reglas de derivación...Área de conocimientoContexto educativoTipo de recurso -
Polígono de cuatro lados. Paralelogramo.
 En la actividad se construye a partir de un polígono de cuatro lados un paralelogramo. Se comprueba gráfica y empíricamente (Tales) que lo es.Área de conocimientoContexto educativoTipo de recurso
En la actividad se construye a partir de un polígono de cuatro lados un paralelogramo. Se comprueba gráfica y empíricamente (Tales) que lo es.Área de conocimientoContexto educativoTipo de recurso -
Polígono de cuatro lados. Paralelogramo.
 En la actividad se construye a partir de un polígono de cuatro lados un paralelogramo. Se comprueba gráfica y empíricamente (Tales) que lo es.Área de conocimientoContexto educativoTipo de recurso
En la actividad se construye a partir de un polígono de cuatro lados un paralelogramo. Se comprueba gráfica y empíricamente (Tales) que lo es.Área de conocimientoContexto educativoTipo de recurso


