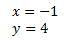Matrices y Sistemas de Ecuaciones Lineales (SEL)
Matrices y Sistemas de Ecuaciones Lineales (SEL)
1. Definición de SEL y su solución
Un sistema de m ecuaciones lineales con n incógnitas (SEL) y coeficientes en un cuerpo K (como los reales o los complejos) es
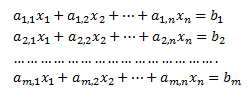
A los elementos ai,j se les denomina coeficientes del SEL y a los b_i términos independientes.
Un ejemplo de un SEL de dos ecuaciones y dos incógnitas es
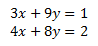
Dimensión del SEL:
-
dimensión cuadrada: si m = n (tiene el mismo número de ecuaciones que de incógnitas).
-
dimensión rectangular: si m ≠ n (no tiene el mismo número de ecuaciones que de incógnitas).
Tipos de SEL (según los términos independientes)
-
Sistema homogéneo (SELH): todos los términos independientes son 0.
-
Sistema completo (SELC) o no homogéneo: alguno de los términos independientes es distinto de 0.
Representación matricial de un SEL
El SEL definido anteriormente se representa matricialmente como
A·X = b
siendo A una matriz de dimensión mxn formada por los coeficientes de las incógnitas, X una matriz de dimensión nx1 (una columna) formada por las incógnitas del sistema y b una matriz de dimensión nx1 formada por los términos independientes del sistema:
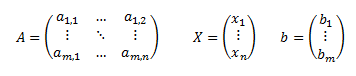
La matriz ampliada del sistema, A*, es la matriz que contiene a la matriz A a la izquierda y a la matriz b a la derecha:
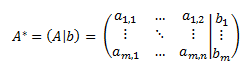
Ejemplo:
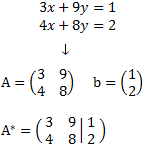
2. Soluciones de un SEL
La solución de un SEL es el conjunto de valores que debe tomar cada incógnita para que todas las ecuaciones del SEL se satisfagan simultáneamente.
Pueden darse las siguientes situaciones:
-
Sistema Incompatible: no existe solución.
-
Sistema Compatible Determinado (SCD): existe una única solución.
-
Sistema Compatible Indeterminado (SCI): existen varias soluciones (infinitas).
Más información: Matrices y SEL's.
Existe un teorema que nos permite saber el tipo de un SEL a partir del rango de las matrices de su representación:
3. Teorema de Rouché-Frobenius
Sea A·X = b un sistema de m ecuaciones lineales con n incógnitas (sobre un cuerpo en general), siendo m y n naturales (no nulos). Entonces,
-
A·X = b es compatible si, y sólo si,
rango( A ) = rango ( A | b ).
-
A·X = b es compatible determinado si, y sólo si,
rango( A ) = n = rango( A | b ).
Enlace: Demostración del Teorema de Rouché-Frobenius
4. Resolución de un SEL
Existen varios métodos para resolver un SEL matricialmente. Los más conocidos son:
4.1.Relga de Cramer:
Mediante el cálculo de determinantes. Este método solo es aplicable cuando el SEL es SCD.
Ejemplo:
El determinante del siguiente sistema es -8 (distinto de 0)
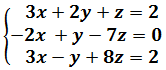
Por la regla de Cramer, el valor de la incógnita número i es el determinante de la matriz H dividido por el determinante de A (que es -8). La matriz H es la que resulta al cambiar la columna i de A por la columna de términos independientes:
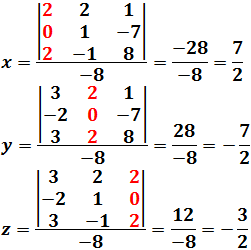
4. 2. Eliminación de Gauss-Jordan:
cálculo de matrices equivalentes para obtener la Forma Escalonada Reducida del sistema.
Ejemplo:
Calculamos la forma escalonada reducida de la matriz ampliada del sistema
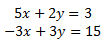
Multiplicamos la primera fila por 1/5 y la segunda por 1/3:
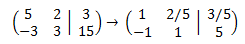
Sumamos a la segunda fila la primera:
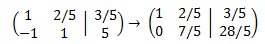
Multiplicamos la segunda fila por 5/7:
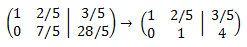
Sumamos a la primera fila la segunda fila multiplicada por -2/5:
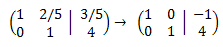
Se deduce que la solución del sistema es
