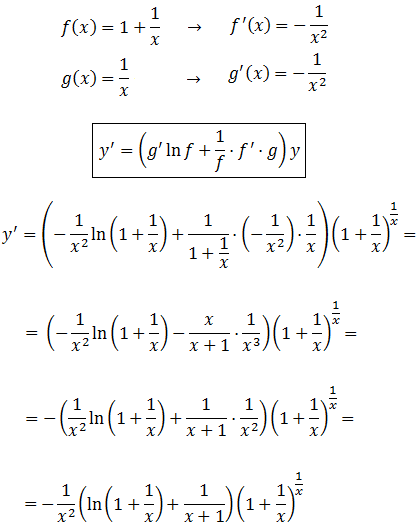Derivada de una función elevada a otra
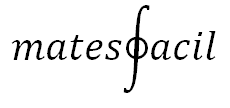
En este artículo vamos a obtener una fórmula para calcular la derivada de una función elevada a otra función, por ejemplo:
1. La fórmula
Sea la función y(x) la que queremos derivar. Supongamos que es de la forma:
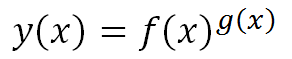
Es decir, la función y(x) es la función f(x) elevada a la función g(x).
Para facilitar la notación, escribimos y, f y g para referirnos a las funciones y(x), f(x) y g(x), respectivamente. Las derivadas de estas funciones las escribiremos como y', f' y g'.
Por tanto, la función es
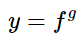
Aplicamos logaritmos y sus propiedades a la igualdad anterior:
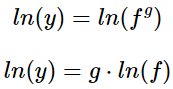
Derivamos en la igualdad (derivada del producto y del logaritmo) aplicando la regla de la cadena:
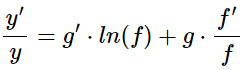
Aislamos y' en la expresión anterior:
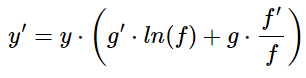
Esta última expresión es la fórmula que usaremos. Sólo tenemos que identificar las funciones f y g, calcular sus derivadas y aplicar la fórmula.
2. Ejemplos de aplicación
Ejemplo 1:
Calculamos la derivada de
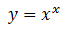
Aplicamos la fórmula:
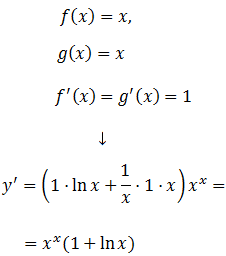
Ejemplo 2:
Calculamos la derivada de
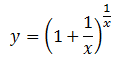
Aplicamos la fórmula: