Ecuaciones irracionales
Una ecuación irracional es aquella en la que aparecen raíces que contienen a la incógnita, es decir, la incógnita se encuentra bajo signos radicales.
Para resolver una ecuación irracional, se elevan ambos lados de la ecuación al orden de la raíz (al cuadrado, al cubo...). Este procedimiento aumenta el grado de la ecuación, por lo que posiblemente estamos añadiendo soluciones. Es por ello por lo que siempre comprobaremos las soluciones.
Otro problema que conlleva esta potenciación, en el caso de las raíces de orden par, es que debemos asegurarnos de que las expresiones de los radicandos son positivas o cero.
Ejemplos
Ecuación 1
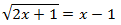
Resolución:
Como tenemos una raíz cuadrada, elevamos al cuadrado ambos lados de la ecuación. No olvidemos que tenemos que aplicar la fórmula del binomio al cuadrado (suma al cuadrado) en el lado derecho.
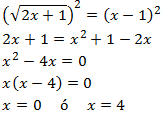
Comprobamos las soluciones:
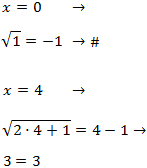
Por tanto, la única solución es x = 4.
Ecuación 2
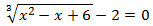
Resolución:
Como tenemos una raíz cúbica, elevamos al cubo ambos lados de la ecuación. Para evitar tener que usar la fórmula del trinomio al cubo, escribimos el -2 al otro lado de la ecuación:
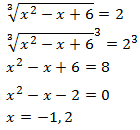
Comprobamos las soluciones:
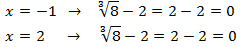
Por tanto, las dos soluciones obtenidas son soluciones de la ecuación irracional.
Más información:
Ecuaciones Resueltas:
- Nivel 1: primeras ecuaciones
- Nivel 2: número de soluciones
- Nivel 3: ecuaciones con paréntesis
- Nivel 4: ecuaciones con fracciones
- Nivel 5: ecuaciones con fracciones y con paréntesis
- Nivel 6: 50 problemas resueltos
Otros:
- Fracciones equivalentes e irreductibles
- Potencias
- Ecuaciones de primer grado
- Problemas con ecuaciones de primer grado
- Problemas de sistemas de ecuaciones
- Ecuaciones de segundo grado
- Problemas de Pitágoras
- Progresiones
- Ecuaciones exponenciales


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


