Teorema del coseno

Teorema del coseno
El teorema del coseno (o teorema de los cosenos) es un resultado de trigonometría que establece la relación de proporcionalidad existente entre las longitudes de lados de un triángulo cualquiera con los cosenos de sus ángulos interiores opuestos.
Sea un triángulo cualquiera con lados a, b y c y con ángulos interiores α, β y γ (son los ángulos opuestos a los lados, respectivamente).
Entonces, se cumplen las relaciones
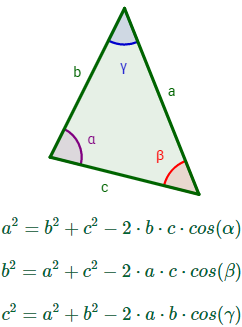
Nota: se dice que es una generalización de Pitágoras porque si uno de los ángulos es recto, el triángulo es rectángulo, siendo la hipotenusa el lado opuesto a dicho ángulo y se obtiene el teorema de Pitágoras al aplicar el del coseno.
Ejemplos de aplicación
Problema 1
Se tiene un triángulo cuyos lados b y c miden 45 y 66 cm respectivamente y cuyo ángulo α mide 47°. Hallar cuánto mide el lado a del triángulo.
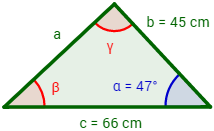
Resolución:
Como queremos calcular el lado a del triángulo, aplicamos la siguiente fórmula del teorema del coseno:
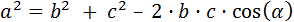
Tenemos los datos necesarios para calcular a, es decir, tenemos b, c y al ángulo α. Por tanto, sustituyendo los datos y haciendo la raíz cuadrada obtenemos:
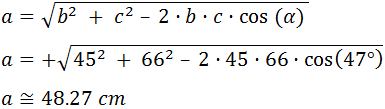
Luego el lado a mide aproximadamente 48.27 cm.
Nota: al hacer la raíz cuadrada hay que escribir el signo ±, pero como a representa una longitud, debe ser positiva.
Problema 2
Si cierto triángulo tiene un lado de 25.5 cm y otro de 37.5 cm y sus respectivos ángulos opuestos son de 37° y 62°, ¿cuánto mide el otro lado?
Resolución:
El triángulo es el siguiente:
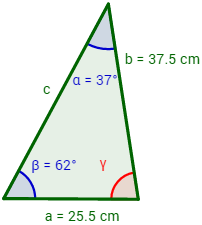
Para hallar el lado c aplicaremos la siguiente fórmula del teorema del coseno:
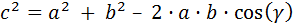
Pero para poder aplicarla, necesitamos conocer el ángulo γ. Esto no supone ningún problema ya que la suma de los ángulos interiores de un triángulo es siempre 180°, por lo que tenemos la ecuación:
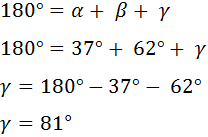
Aplicamos la fórmula:
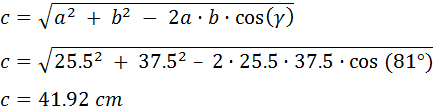
Luego el lado c mide 41.92 cm.
Enlaces:
-
Ecuaciones Resueltas:
- Nivel 1: primeras ecuaciones
- Nivel 2: número de soluciones
- Nivel 3: ecuaciones con paréntesis
- Nivel 4: ecuaciones con fracciones
- Nivel 5: ecuaciones con fracciones y con paréntesis
- Nivel 6: 50 problemas resueltos
Otros:
- Fracciones equivalentes e irreductibles
- Potencias
- Ecuaciones de primer grado
- Problemas con ecuaciones de primer grado
- Problemas de sistemas de ecuaciones
- Ecuaciones de segundo grado
- Problemas de Pitágoras
- Progresiones
- Ecuaciones exponenciales


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


