Proporcionalidad y regla de tres
Proporcionalidad directa
Dos magnitudes a y b son directamente proporcionales cuando existe una constante k tal que
a/b = k
La constante k se denomina constante de proporcionalidad o razón.
Se dice que a y b mantienen una relación de proporcionalidad directa.
En la proporcionalidad directa, cuando una de las magnitudes cambia, la otra también debe hacerlo de modo que su razón se mantenga constante.
Ejemplo:
En un movimiento con velocidad constante v, la distancia recorrida viene dada por la ecuación
distancia = v·tiempo
La distancia es directamente proporcional al tiempo puesto que
distancia/tiempo = v
La velocidad es la constante de proporcionalidad.
Cuando el tiempo aumenta, la distancia también lo hace y viceversa.
Proporcionalidad inversa
Dos magnitudes a y b son inversamente proporcionales cuando existe una constante k tal que
a·b= k
La constante k se denomina constante de proporcionalidad.
En esta proporcionalidad, cuando una de las magnitudes aumenta, la otra disminuye y viceversa.
Ejemplo:
Siguiendo el ejemplo anterior, el tiempo es inversamente proporcional a la velocidad. Cuando la velocidad aumenta, el tiempo necesario para recorrer una misma distancia disminuye.
Regla de tres
Para resolver problemas de proporcionalidad aplicaremos una regla de tres directa o inversa.
Problema 1
El precio de un paquete de 13 rotuladores es de 9.75€. Calcular cuántos rotuladores podemos comprar por el precio de 15.75€.
Solución:
Se trata de una relación de proporcionalidad directa: cuantos más rotuladores compramos, mayor es el precio total.
Llamamos x al número de rotuladores que queremos comprar y que desconocemos:
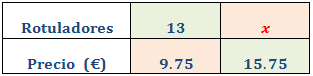
Como es proporcionalidad directa, aplicamos una regla de tres directa:
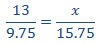
Despejamos la x:
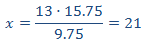
Hemos pintado las celdas en forma de aspa ya que podemos obtener la fórmula anterior directamente multiplicando los dos recuadros verdes y dividiendo entre el rojo (el que no tiene la x).
Por tanto, podemos comprar 21 rotuladores por el precio total de 15.75€.
Problema 2
Tres personas tardan 12 horas en pintar un muro. Calcular cuántas personas se necesitan si se quiere finalizar la tarea en tan solo 4 horas.
Solución:
Es una proporcionalidad inversa: cuantos más trabajadores, menos tiempo.
Llamamos x al número de personas:
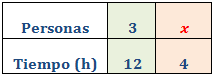
Como es una proporcionalidad inversa, aplicamos una regla de tres inversa:
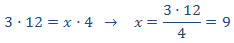
Se necesitan 9 personas.
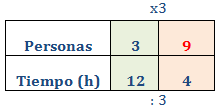
Notemos que para pasar de la primera columna a la segunda multiplicamos por 3 en la primera fila y dividimos entre 3 en la segunda:
Más información y problemas:
-
Calculadora de porcentajes online (proporcionalidad simple)


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


