Problemas de trigonometría: seno y coseno
Si conocemos dos lados de un triángulo rectángulo, podemos calcular el otro lado aplicando el teorema de Pitágoras. Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno.
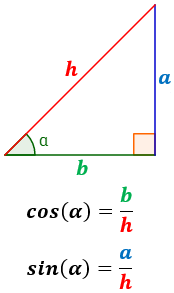
El coseno de un ángulo α se define como el cociente del lado contiguo al ángulo α y la hipotenusa.
De forma análoga, el seno de α se define como el cociente del lado opuesto al ángulo α y la hipotenusa.
Nota: si cambiamos de ángulo, cambian los numeradores:
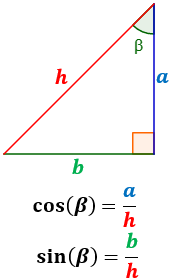
Normalmente, para referirnos al seno de α podemos escribir sin(α), sen(α) ó seno(α). Y para el coseno, cos(α) ó coseno(α).
La tangente del ángulo α es el cociente del seno y del coseno de dicho ángulo:
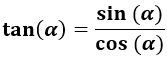
La tangente es el cociente del lado opuesto y del lado contiguo.
La tangente del ángulo α puede escribirse como tan(α) y como tg(α), entre otras.
Ejemplos de aplicación
Problema 1: se desea sujetar un poste de 20 metros de altura con un cable que parte de la parte superior del mismo hasta el suelo de modo que forme un ángulo de 30º. Calcular el precio del cable si cada metro cuesta 12$.
Solución:
Como conocemos el lado opuesto, a=20m, utilizamos el seno para calcular la hipotenusa del triángulo:
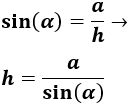
Sustituimos el ángulo y el lado:
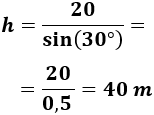
Luego el cable debe medir 40 metros y su precio es de 480$:
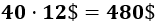
Problema 2: calcular la altura, a, de un árbol sabiendo que, si nos situamos 8 metros de la base del tronco, vemos la parte superior de su copa en un ángulo de 36.87º.
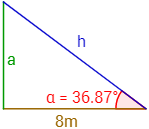
Solución:
Como la altura, a, es el cateto opuesto al ángulo, utilizaremos el seno:
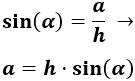
Pero como necesitamos calcular la hipotenusa, h, del triángulo, utilizamos el coseno:
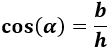
Sustituimos los datos:
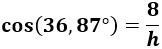
La hipotenusa mide
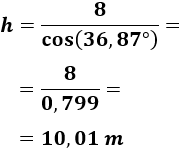
Por tanto, la altura del árbol es
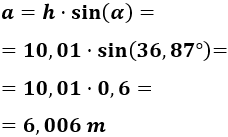
Más información y problemas:


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


