Dominio y Recorrido (de una función)
Dominio y recorrido de una función
1. Dominio y codominio
Una función, f, es una ley entre dos conjuntos de números: el dominio y el codominio. A cada número del dominio le hace corresponder un único número del codominio. Esta ley es una correspondencia unívoca.
Ejemplo:
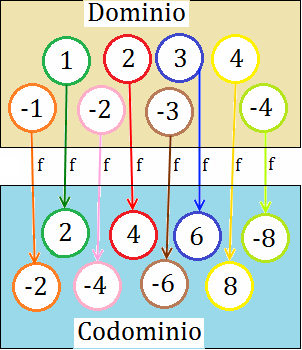
En el ejemplo, el dominio es el conjunto
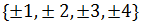
El codominio es el conjunto
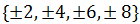
La expresión de la función es
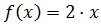
ya que lo que hace la función es multiplicar por dos cada número del dominio.
Podemos observar cómo a cada elemento del dominio le corresponde un único elemento del codominio.
2. Recorrido o Imagen
Sea x un elemento del dominio, llamamos imagen de x mediante la función f a f(x), es decir, al elemento del codominio que le asigna la función f.
En la función del ejemplo:
-
La imagen de 1 es
f(1) = 2·1 = 2
-
La imagen de -1 es
f(-1) = 2·(-1) = -2
-
La imagen de 2 es
f(2) = 2·2 = 4
-
La imagen de -2 es
f(2) = 2·(-2) = -4
-
Es análogo para los restantes elementos del dominio.
Llamamos conjunto imagen (o simplemente imagen) o recorrido de la función f al conjunto de elementos del codominio que son la imagen de algún (o más) elemento del dominio.
Es decir, si y es un elemento de la imagen de f, entonces existe al menos un elemento, x, del dominio de f tal que
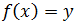
Nota: el conjunto imagen de una función es un subconjunto del codominio. En muchos textos no se realiza ninguna distinción entre los conceptos de codominio y recorrido (o imagen) y se utilizan ambos términos con el significado que le hemos dado al de recorrido (o imagen).
En el ejemplo anterior, el codominio coincide con la imagen.
Enlaces con problemas de funciones:
- Dominio y recorrido (1)
- Dominio y recorrido (2)
- Funciones lineales
- Funciones cuadráticas
- Rectas y parábolas
- Funciones polinómicas
- Funciones definidas a trozos (1)
- Funciones definidas a trozos (2)
- Problemas de funciones (1)
- Problemas de funciones (2)
- Funciones continuas (1)
- Funciones continuas (2)
- Función inversa (1)
- Función inversa (2)
- Función inyectiva, sobreyectiva y biyectiva
- Asíntotas (1)
- Asíntotas (2)
- Máximos y mínimos (1)
- Máximos y mínimos (2)
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Problemas de optimizar (1)
- Problemas de optimizar (2)
- Límites (1)
- Límites (2)
- Función par y función impar
- Cálculo de derivadas
- Teorema del emparedado


