Estudio de la continuidad, extremos, monotonía y curvatura de una función
Estudio de la continuidad, monotonía, existencia de extremos (máximos y mínimos) y curvatura (convexa o cóncava).
(aplicaciones del cálculo diferencial)
Estudio de la función:
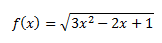
1. Dominio, recorrido y continuidad:
Como la función es una raíz cuadrada, el radicande debe ser mayor o igual que 0. Resolvemos la inecuación:
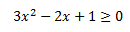
La desigualdad siempre se cumple ya que la ecuación de segundo grado no tiene soluciones (reales) y, por tanto, la función no cambia de signo, manteniéndose siempre en los reales no negativos.
Por tanto, el dominio de la función es todos los reales.
El recorrido de la función la calcularemos cuando sepamos si tiene máximos o mínimos.
Puesto que la función es una raíz cuadrada, es continua en todos los puntos de su dominio, es decir, en todos los reales.
Más información:
2. Monotonía y extremos
Calculamos la derivada de la función aplicando la Regla de la cadena:
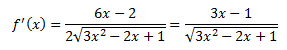
Los posibles extremos de la función son los puntos para los cuales la primera derivada se anula (puntos críticos). Igualamos la derivada a 0 y resolvemos la ecuación:
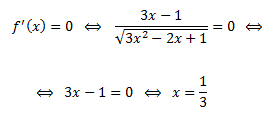
Por tanto, el único punto crítico es x = 1/3.
Para saber si este punto es un extremos, podemos:
-
aplicar el criterio de la segunda derivada
-
o bien, aplicar el criterio de la primera derivada para estudiar la monotonía (creciente o decreciente) y deducir si es un extremo y qué tipo.
Nosotros aplicaremos el criterio de la primera derivada porque así sabemos también la monotonía de la función (con menos cálculos).
El punto crítico divide al dominio en dos intervalos:
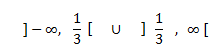
Estudiamos el primera derivada en un punto cualquiera de cada uno de estos intervalos:
-
Para el primer intervalo escogemos el punto x = 0. La derivada en x = 0 es f'(0)=-1.
Como es negativa, por el criterio de la primera derivada, la función es decreciente en dicho intervalo.
-
Para el segundo intervalo escogemos el punto x = 1. La derivada es f'(1) > 0. Por tanto, la función es creciente en dicho intervalo.
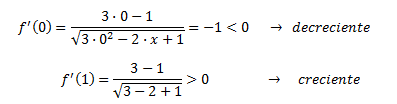
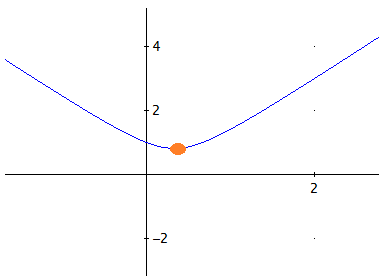
Como la función es decreciente en el intervalo de la izquierda y crececiente en el de la derecha, deducimos que en el punto x = 1/3 hay un extremo y es un mínimo.
El mínimo es un extremo absoluto.
Además, ahora sabemos que el recorrido de la función es todos los reales mayores que f(1/3).
Más información:
3. Curvatura de la función
Calculamos la segunda derivada:
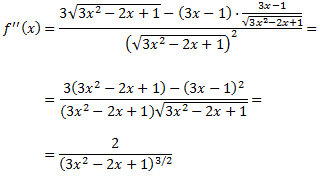
Si la curvatura de la función cambia en algún punto, entonces la segunda derivada se anula en dicho punto (punto de inflexión). Por eso, igualamos la segunda derivada a cero para encontrar los candidatos:
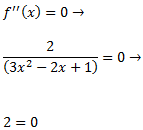
Como la ecuación no tiene solución, no hay puntos de inflexión y, por tanto, la función es cóncava o convexa en todo su dominio.
Observando la gráfica, sabemos que la función es convexa.
Más información:



