RECURSOS DE APRENDIZAXE
-
MA1 - Tarea 6.2: Especies exóticas invasoras

Curso: 1º Enseñanza: Bachillerato Nombre asignatura/materia: Matemáticas Aplicadas a las Ciencias Sociales I Tipo tarea: Individual Descripción: En esta tarea, estudiaremos el comportamiento de dos especies exóticas invasoras, utilizando los conceptos de límite y derivada de una función.
Contexto educativoTipo de recurso -
Máximos y mínimos (funciones)
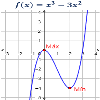
Definimos máximos y mínimos relativos y absolutos de una función, enunciamos el criterio de la primera derivada y explicamos cómo aplicarlo para deducir la existencia de extremo. Con ejemplos. Enlaces con problemas de funciones: Dominio y recorrido (1) Dominio y recorrido (2) Funciones lineales Funciones cuadráticas Rectas y parábolas Funciones polinómicas Funciones definidas a trozos (1) Funciones definidas a trozos (2) Problemas de funciones (1) Problemas de funciones (2) Funciones continu...
Área de coñecementoContexto educativoTipo de recurso -
MT1 - Práctica 4.1: Análisis II

Curso: 1º Enseñanza: Bachillerato Nombre asignatura/materia: Matemáticas I Tipo tarea: Ejercicio / Actividad de práctica Descripción: Te ofrecemos un cuestionario compuesto por varias preguntas referidas a los conceptos y procedimientos básicos de la unidad "Análisis II".
Contexto educativoTipo de recurso -
MT2 - Tema 4.1: Derivadas: Derivada. Interpretación geométrica. Cálculo de derivadas

Curso 2º - Enseñanza Bachillerato Nombre asignatura/materia: Matemáticas II
Contexto educativoTipo de recurso -
MA2 - Tema 3.3: Análisis I: Derivada de una función.

Curso 2º - Enseñanza Bachillerato Nombre asignatura/materia: Matemáticas Aplicadas a las Ciencias Sociales II
Contexto educativoTipo de recurso -
PAU_MA - Tema 2.3: Funciones: Cálculo de derivadas y aplicaciones

Enseñanza PAU Pruebas de Acceso a la Universidad para mayores de 25 años Materia: Matemáticas Aplicadas a las Ciencias Sociales
Tipo de recurso -
Polinomios de Taylor
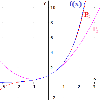
En este documento definimos el polinomio de Taylor de una función de una variable y enunciamos el teorema de la fórmula de Taylor con resto de Lagrange. También, calculamos los polinomios de grado 2 y grado 5 de la función exponencial y proporcionamos las cotas del error obtenido en la aproximación para el intervalo _0,1_. Recursos de Cálculo Diferencial: Teorema de Taylor con resto de Lagrange Introducción al Cálculo Diferencial (teoría) Tabla de derivadas elementales y reglas de derivación...
Área de coñecementoContexto educativoTipo de recurso -
Polinomios de Taylor
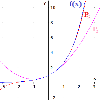
En este documento definimos el polinomio de Taylor de una función de una variable y enunciamos el teorema de la fórmula de Taylor con resto de Lagrange. También, calculamos los polinomios de grado 2 y grado 5 de la función exponencial y proporcionamos las cotas del error obtenido en la aproximación para el intervalo _0,1_. Recursos de Cálculo Diferencial: Teorema de Taylor con resto de Lagrange Introducción al Cálculo Diferencial (teoría) Tabla de derivadas elementales y reglas de derivación...
Área de coñecementoContexto educativoTipo de recurso -
MA2 - Elementos Comunes Unidad 4: Análisis II

Curso 2º - Enseñanza Bachillerato Nombre asignatura/materia: Matemáticas II
Contexto educativoTipo de recurso -
MA2 - Elementos Comunes Unidad 3: Análisis I.

Curso 2º - Enseñanza Bachillerato Nombre asignatura/materia: Matemáticas Aplicadas a las Ciencias Sociales II
Contexto educativoTipo de recurso -
La Regla de L'Hôpital
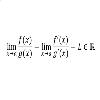
En este documento enunciamos la Regla de L'Hôpital y la aplicamos para calculas dos límites. Más ejemplos de aplicación: La Regla de L'Hôpital. Recursos de Cálculo Diferencial: Introducción al Cálculo Diferencial (teoría) Tabla de derivadas elementales y reglas de derivación (PDF) Cálculo de derivadas (Regla de la cadena) Cálculo de extremos relativos Demostración del Criterio de la Primera Derivada Demostración del Criterio de la Segunda Derivada Demostración de la Condición Necesaria de Ex...
Área de coñecementoContexto educativoTipo de recurso -
MA1 - Tema 6.4: Análisis II: Función derivada. Reglas de derivación

Curso 1º - Enseñanza Bachillerato Nombre asignatura/materia: Matemáticas Aplicadas a las Ciencias Sociales I
Contexto educativoTipo de recurso -
MA1 - Tema 6.3: Análisis II: Derivada de una función en un punto. Interpretación geométrica

Curso 1º - Enseñanza Bachillerato Nombre asignatura/materia: Matemáticas Aplicadas a las Ciencias Sociales I
Contexto educativoTipo de recurso -
MT1 - Práctica 4.1: Análisis II

Curso: 1º Enseñanza: Bachillerato Nombre asignatura/materia: Matemáticas I Tipo tarea: Ejercicio / Actividad de práctica Descripción: Te ofrecemos un cuestionario compuesto por varias preguntas referidas a los conceptos y procedimientos básicos de la unidad "Análisis II".
Contexto educativoTipo de recurso -
MT2 - Tarea 4.2: La Estación Espacial Internacional

Curso: 2º Enseñanza: Bachillerato Nombre asignatura/materia:Matemáticas II Tipo tarea:Individual Descripción: En esta tarea aplicarás tus conocimientos del cálculo diferencial a la planificación y desarrollo de una misión espacial.
Contexto educativoTipo de recurso -
MT2 - Práctica 4.1: Derivadas

Curso: 2º Enseñanza: Bachillerato Nombre asignatura/materia: Matemáticas II Tipo tarea: Ejercicio / Actividad de práctica Descripción: Te ofrecemos una serie de ejercicios referidos a los conceptos y procedimientos básicos de la unidad: "Derivadas".
Contexto educativoTipo de recurso -
Derivada de una función elevada a otra función
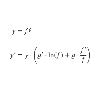
En este documento vamos a calcular una fórmula para obtener la derivada de una función elevada a otra función: y(x) = f(x)^(g(x)). Aplicaremos las propiedades de los logaritmos (logaritmo de una potencia) para evitar el exponente . Después, derivamos la igualdad obtenida (derivada del logaritmo y regla de la cadena). Finalmente, aislamos la derivada de y obteniendo una fórmula. El documento contiende dos ejemplos de aplicación de la fórmula.
Área de coñecementoContexto educativoTipo de recurso -
teorema_de_rolle
Enunciado y ejemplo de aplicación del teorema de Rolle. Relacionados: Criterio de la primera derivada (con demostración) Regla de L'Hôpital Problemas de extremos relativos Problemas de Optimizar
Área de coñecementoContexto educativoTipo de recurso


