PROCOMÚN
Mostrando os resultados do 181 ao 200 dun total de 280
-
Proyecciones
 El concepto de proyección determina el proceso por el que se obtiene una imagen sobre un plano de una figura bidimensional o tridimensional situada en el espacio. Por tanto, las proyecciones se obtienen trazando rayos proyectantes paralelos entre sí por los puntos más significativos de las figuras hasta cortar el plano del dibujo. Con esta escena podremos manipular y visualizar proyecciones.Área de coñecementoContexto educativoTipo de recursoColecciones
El concepto de proyección determina el proceso por el que se obtiene una imagen sobre un plano de una figura bidimensional o tridimensional situada en el espacio. Por tanto, las proyecciones se obtienen trazando rayos proyectantes paralelos entre sí por los puntos más significativos de las figuras hasta cortar el plano del dibujo. Con esta escena podremos manipular y visualizar proyecciones.Área de coñecementoContexto educativoTipo de recursoColecciones -
Proyección de la semiesfera en el plano
 La escena permite ver cómo la proyección estereográfica desde el entro de una semiesfera asocia a cada punto de la superficie de la misma un punto del plano que se encuentra bajo ella formando una correspondencia biunívoca. De igual manera, permite proyectar meridianos, paralelos y recorridos cualesquiera.Área de coñecementoContexto educativoTipo de recursoColecciones
La escena permite ver cómo la proyección estereográfica desde el entro de una semiesfera asocia a cada punto de la superficie de la misma un punto del plano que se encuentra bajo ella formando una correspondencia biunívoca. De igual manera, permite proyectar meridianos, paralelos y recorridos cualesquiera.Área de coñecementoContexto educativoTipo de recursoColecciones -
Propiedades de los números
 Al disponer ordenadamente los números en una tabla se pueden observar ciertas regularidades que permiten realizar divisiones, obtener divisores, calcular múltiplos, etc.Área de coñecementoContexto educativoTipo de recursoColecciones
Al disponer ordenadamente los números en una tabla se pueden observar ciertas regularidades que permiten realizar divisiones, obtener divisores, calcular múltiplos, etc.Área de coñecementoContexto educativoTipo de recursoColecciones -
Polinomio de Taylor
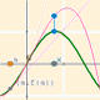 Applet Descartes que permite, dada una función y un punto, calcular el polinomio de Taylor hasta de cuarto grado. Visualiza la aproximación de la función por dicho polinomio y las correspondiente gráficas. Sus controles permiten modificar las condiciones iniciales.Área de coñecementoContexto educativoTipo de recursoColecciones
Applet Descartes que permite, dada una función y un punto, calcular el polinomio de Taylor hasta de cuarto grado. Visualiza la aproximación de la función por dicho polinomio y las correspondiente gráficas. Sus controles permiten modificar las condiciones iniciales.Área de coñecementoContexto educativoTipo de recursoColecciones -
Polígonos estrellados
 A partir de un polígono regular convexo se puede obtener un polígono estrellado. Para ello se unen los vértices no consecutivos, según un salto establecido (paso), de tal forma que se recorren todos los vértices del polígono. Es decir, se empieza por un vértice cualquiera uniendo este con el siguiente vértice según el paso establecido, a continuación se une este con el siguiente, siempre respetando el paso, y así sucesivamente hasta llegar de nuevo al vértice de partida.Área de coñecementoContexto educativoTipo de recursoColecciones
A partir de un polígono regular convexo se puede obtener un polígono estrellado. Para ello se unen los vértices no consecutivos, según un salto establecido (paso), de tal forma que se recorren todos los vértices del polígono. Es decir, se empieza por un vértice cualquiera uniendo este con el siguiente vértice según el paso establecido, a continuación se une este con el siguiente, siempre respetando el paso, y así sucesivamente hasta llegar de nuevo al vértice de partida.Área de coñecementoContexto educativoTipo de recursoColecciones -
Pistones en movimiento
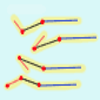 Muestra gráfica de la sincronización de cuatro pistones.Área de coñecementoContexto educativoTipo de recursoColecciones
Muestra gráfica de la sincronización de cuatro pistones.Área de coñecementoContexto educativoTipo de recursoColecciones -
Pentominó y tetrahexes
 Los rompecabezas son juegos muy valorados, desde el punto de vista educativo, porque a la vez que fomentan la creatividad, el dasarrollo de las capacidades de análisis y síntesis, la visión espacial, las estructuras y los movimientos geométricos... son entretenidos y resultan divertidos para la gran mayoría de las personas, de cualquier edad. Parece, por ello, muy conveniente utilizar estos juegos por sus aspectos motivadores y formativos en el Taller de Matemáticas donde, además, se puede pr...Área de coñecementoContexto educativoTipo de recursoColecciones
Los rompecabezas son juegos muy valorados, desde el punto de vista educativo, porque a la vez que fomentan la creatividad, el dasarrollo de las capacidades de análisis y síntesis, la visión espacial, las estructuras y los movimientos geométricos... son entretenidos y resultan divertidos para la gran mayoría de las personas, de cualquier edad. Parece, por ello, muy conveniente utilizar estos juegos por sus aspectos motivadores y formativos en el Taller de Matemáticas donde, además, se puede pr...Área de coñecementoContexto educativoTipo de recursoColecciones -
Pentágono regular áureo
 Estudio interactivo y lúdico de la proporción áurea.Área de coñecementoContexto educativoTipo de recursoColecciones
Estudio interactivo y lúdico de la proporción áurea.Área de coñecementoContexto educativoTipo de recursoColecciones -
Parchís y dados cargados
 Simulación de los resultados obtenidos al lanzar un dado que está trucado, con posibilidad de cargar cada una de sus caras con un peso de 1 a 10.Área de coñecementoContexto educativoTipo de recursoColecciones
Simulación de los resultados obtenidos al lanzar un dado que está trucado, con posibilidad de cargar cada una de sus caras con un peso de 1 a 10.Área de coñecementoContexto educativoTipo de recursoColecciones -
Para representar funciones
 Se trata de una utilidad que permite representar cualquier función. Tiene la particularidad de que se puede modificar la escala de los ejes, manteniendo la misma o distinta escala para así analizar mejor algunas propiedades de la función representada. También se puede centrar la gráfica en el punto que se desee.Área de coñecementoContexto educativoTipo de recursoColecciones
Se trata de una utilidad que permite representar cualquier función. Tiene la particularidad de que se puede modificar la escala de los ejes, manteniendo la misma o distinta escala para así analizar mejor algunas propiedades de la función representada. También se puede centrar la gráfica en el punto que se desee.Área de coñecementoContexto educativoTipo de recursoColecciones -
Otro transportador gráfico
 Enseñanza del uso del transportador de ángulos de forma dinámica e interactiva.Área de coñecementoContexto educativoTipo de recursoColecciones
Enseñanza del uso del transportador de ángulos de forma dinámica e interactiva.Área de coñecementoContexto educativoTipo de recursoColecciones -
Un problema clásico de maximización de un volumen
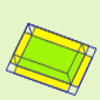 Dada un pieza resctangular de dimensiones a por b, recortar cuatro equinas iguales (cuadradas) de lado x y construir una caja sin tapa de volumen máximo. La escena calcula el volumen obtenido al variar x fijados a y b. Además permite girar la figura para observarla mejor.Área de coñecementoContexto educativoTipo de recursoColecciones
Dada un pieza resctangular de dimensiones a por b, recortar cuatro equinas iguales (cuadradas) de lado x y construir una caja sin tapa de volumen máximo. La escena calcula el volumen obtenido al variar x fijados a y b. Además permite girar la figura para observarla mejor.Área de coñecementoContexto educativoTipo de recursoColecciones -
Ortoedro con cubos
 El desarrollo de los temas dedicados a la Geometría del espacio requiere, para mejorar la comprensión de los mismos, estar familiarizado con la representación en el plano del espacio tridimensional. En este trabajo relacionamos la representación del ortoedro con su volumen con el cubo unidad.Área de coñecementoContexto educativoTipo de recursoColecciones
El desarrollo de los temas dedicados a la Geometría del espacio requiere, para mejorar la comprensión de los mismos, estar familiarizado con la representación en el plano del espacio tridimensional. En este trabajo relacionamos la representación del ortoedro con su volumen con el cubo unidad.Área de coñecementoContexto educativoTipo de recursoColecciones -
Un grupo de frisos
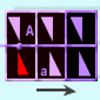 Mediante esta escena pueden analizarse dos de los movimientos en el plano: traslaciones y giros, así como la obtención de frisos como combinación de estos movimientos.Área de coñecementoContexto educativoTipo de recursoColecciones
Mediante esta escena pueden analizarse dos de los movimientos en el plano: traslaciones y giros, así como la obtención de frisos como combinación de estos movimientos.Área de coñecementoContexto educativoTipo de recursoColecciones -
Un cuadrado mágico
 Un cuadrado mágico se obtiene colocando una serie de números naturales en una matriz cuadrada de tal forma que todas las filas, todas las columnas y las diagonales sumen el mismo número: la constante mágica. Generalmente suelen colocarse los números entre 1 y n^2, siendo n el número de filas y columnas del cuadrado. A este número n se le denomina orden del cuadrado mágico. En esta actividad se propone un cuadrado mágico de orden 3, es decir 3 filas por 3 columnas.Área de coñecementoContexto educativoTipo de recursoColecciones
Un cuadrado mágico se obtiene colocando una serie de números naturales en una matriz cuadrada de tal forma que todas las filas, todas las columnas y las diagonales sumen el mismo número: la constante mágica. Generalmente suelen colocarse los números entre 1 y n^2, siendo n el número de filas y columnas del cuadrado. A este número n se le denomina orden del cuadrado mágico. En esta actividad se propone un cuadrado mágico de orden 3, es decir 3 filas por 3 columnas.Área de coñecementoContexto educativoTipo de recursoColecciones -
Triángulos rectángulos en el geoplano
 Construcción de triángulos en un panel que simula el Geoplano.Área de coñecementoContexto educativoTipo de recursoColecciones
Construcción de triángulos en un panel que simula el Geoplano.Área de coñecementoContexto educativoTipo de recursoColecciones -
Triángulo equilátero por dos rectas y un punto exterior a ellas
 RECTAS PARALELAS Dado un punto fijo y dos rectas paralelas, construir un triángulo equilátero con dos vértices situados cada uno en una de las rectas y el tercero en el punto fijo.Área de coñecementoContexto educativoTipo de recursoColecciones
RECTAS PARALELAS Dado un punto fijo y dos rectas paralelas, construir un triángulo equilátero con dos vértices situados cada uno en una de las rectas y el tercero en el punto fijo.Área de coñecementoContexto educativoTipo de recursoColecciones -
Trazado de las rectas notables de un triángulo
 Trazado de las rectas notables de un triángulo apoyada por una colección de ejercicios interactivos.Área de coñecementoContexto educativoTipo de recursoColecciones
Trazado de las rectas notables de un triángulo apoyada por una colección de ejercicios interactivos.Área de coñecementoContexto educativoTipo de recursoColecciones -
Transportador gráfico de ángulos
 Medida de ángulos en escenas reales.Área de coñecementoContexto educativoTipo de recursoColecciones
Medida de ángulos en escenas reales.Área de coñecementoContexto educativoTipo de recursoColecciones -
Transformaciones complejas elementales
 Las funciones complejas requerirían para su visualización cuatro dimensiones: dos para pintar los puntos del dominio y otras dos para la imagen. Por ello es más frecuente interpretar estas funciones como aplicaciones del plano en sí mismo, es decir, como transformaciones del plano. En esta escena se muestra cómo se transforman algunos subconjuntos sencillos del plano (recta y circunferencia) por las funciones complejas elementales.Área de coñecementoContexto educativoTipo de recursoColecciones
Las funciones complejas requerirían para su visualización cuatro dimensiones: dos para pintar los puntos del dominio y otras dos para la imagen. Por ello es más frecuente interpretar estas funciones como aplicaciones del plano en sí mismo, es decir, como transformaciones del plano. En esta escena se muestra cómo se transforman algunos subconjuntos sencillos del plano (recta y circunferencia) por las funciones complejas elementales.Área de coñecementoContexto educativoTipo de recursoColecciones


