Sistema de numeración octal
El sistema decimal es un sistema de numeración posicional. Cuando nos enseñan los números por primera vez, éste es el sistema que se emplea y sin duda es el que más se usa en matemáticas. Sin embargo, hay otros sistemas de numeración que, debido a sus aplicaciones prácticas, también son importantes. Tal es el caso del sistema octal, que se utiliza a veces en informática.
Los símbolos que se usan en este sistema son:
0, 1, 2, 3, 4, 5, 6, 7
Cambio de base 10 a base 8
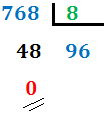
Veamos el método para pasar del sistema decimal al sistema octal mediante un ejemplo. Escribiremos el número \( 768_{(10}\) (base 10) en base 8:
-
Dividimos el número entre 8:
-
Si el cociente es mayor o igual que 8, lo dividimos entre 8.
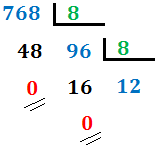
En nuestro caso, el cociente es 96 (mayor que 8), por lo que lo dividimos de nuevo:
-
Continuamos así hasta obtener un cociente menor que 8.
En nuestro caso, el cociente es 12 (mayor que 8), así que lo dividimos de nuevo:
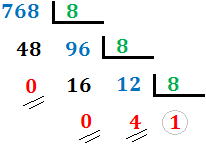
El cociente es 1, menor que 8, con lo que hemos terminado el proceso. Hemos indicado los restos con dos rayas y el último cociente con una circunferencia.
-
El número en base 8 es:
(Último cociente) (Último resto) (Penúltimo resto)... (Segundo resto) (Primer resto).
En nuestro caso,
-
El último cociente es 1.
-
El último resto es 4.
-
El penúltimo resto es 0.
-
El primer resto es 0.
Por tanto, el número 768 en base octal es 1400. Es decir,
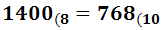
-
Cambio de base 8 a base 10
El método que seguiremos para pasar un número en base octal a base decimal es:
-
De derecha a izquierda: multiplicamos la primera cifra por 1 (1 es 8 elevado a 0) ; la segunda, por 8 (8 es 8 elevado a 1); la tercera, por 8 elevado a 2; la cuarta, por 8 elevado a 3. Y así hasta que hayamos multiplicado todas las cifras.
-
Sumamos cada uno de los valores obtenidos.
Ejemplo:

Enlaces:


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


