Límites con indeterminaciones
Cálculo de límites con indeterminaciones
En ocasiones, al calcular límites encontramos ciertas expresiones cuyos valores no conocemos a priori. Son las llamadas indeterminaciones. Para algunas de ellas existen reglas que nos permiten calcular su valor (como en el caso de 1 elevado a infinito). Pero la mayoría de las indeterminaciones no se resuelven de un modo tan directo, sino que debemos realizar una serie de operaciones o cálculos para poder determinar sus valores.
Debemos decir que en realidad, el cálculo diferencial nos proporciona un método muy efectivo y sencillo bajo ciertas condiciones: la Regla de L'Hôpital. Pero no emplearemos esta regla ya que tenemos una sección especialmente dedicada a ella: Regla de L'Hôpital
Indeterminaciones
1. Infinito dividido infinito: ∞/∞
Puede aparecer en cocientes muy variados: polinomios, raíces, exponenciales... En cada caso se procederá de forma distinta.
2. Diferencia de infinitos: ∞ - ∞
Suele ocurrir cuando tenemos una resta de raíces o de exponenciales. En el primer caso, se multiplica y divide por el conjugado (si las raíces son cuadradas). En el segundo, multiplicamos y dividimos por la exponencial de base mayor.
3. 1 elevado a infinito: 1^∞
Aplicamos la siguiente fórmula:
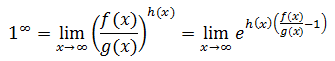
donde las funciones f, g y h las conocemos (la fórmula es la segunda igualdad).
4. Cociente de ceros: 0/0
Suele aparecer en los límites en un punto finito cuando el denominador se anula. Normalmente será un polinomio y podremos factorizarlo.
5. Infinito elevado a 0: ∞^0
Usamos los logaritmos para aprovechar sus propiedades, que son
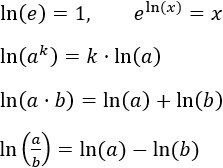
6. Cero elevado a cero: 0^0
Aparece en las exponenciales. Usamos logaritmos como en el caso anterior.
7. Cero por infinito: 0·∞
Aparece en funciones de tipo muy variado.
Enlaces:


Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.


