Cálculo de la Raíz Cuadrada
Cálculo de Ráices Cuadradas
Vamos a ver las partes de una raíz cuadrada y el algoritmo (método) para calcular la raíz cuadrada de un número.
Partes de una raíz cuadrada:
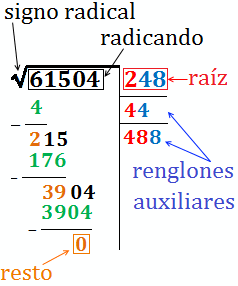
El radicando es el número cuya raíz queremos calcular. Es decir, si b es el radicando y a es la raíz de b, entonces a al cuadrado es b.
El radicando se escribe bajo el signo radical. Por ejemplo, si el radicando es 4, entonces la raíz cuadrada es 2 ya que 2 al cuadrado es 4.
Si la raíz cuadrada no es número exacto (o se quiere calcular la raíz con un número determinado de decimales), entonces, el cuadrado de la raíz calculada no es exactamente el radicando. El resto es el resultado de la resta "radicando" menos "raíz al cuadrado".
Los renglones auxiliares se utilizan para calcular la raíz.
Algoritmo:
Veamos el algoritmo para calcular raíces cuadradas exactas (sin decimales).
Explicaremos el método mientras calculamos la raíz de 61504:
-
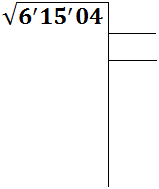
Agrupamos las cifras del radicando en pares (de dos en dos) de derecha a izquierda. Si hay un número impar de cifras, el primer par (el de la izquierda) sólo será un número (como en nuestro caso):
-
Buscamos el mayor número cuyo cuadrado se aproxime al primero de los pares (de izquierda a derecha), es decir, que se aproxime o sea igual que 6.
El cuadrado de 2 es 4 y el cuadrado de 3 es 9. El número 4 es menor que 6 y el número 9 es demasiado grande.
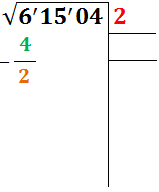
Escribimos un 2 en la parte derecha y su cuadrado, 4, debajo del 6:

Calculamos la resta 6-4 = 2:
-
Escribimos el doble de la raíz (primer renglón) en un nuevo renglón, es decir, escribimos el doble de 2 que es 4:
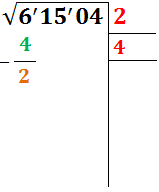
Y bajamos el par siguiente en la parte izquierda, es decir, bajamos 15:
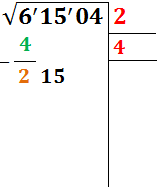
-
Buscamos un número x para que al añadirlo a la derecha del renglón inferior y multiplicar este número por x, se aproxime al número de la parte izquierda (por debajo):
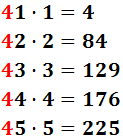
El número que más se aproxima (sin pasarse) a 215 es 176. Es el resultado del producto 44·4 = 176. Escribimos el 4 en la parte derecha en el primer renglón y en el inferior:
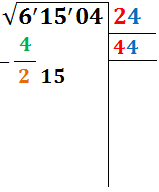
Escribimos también el resultado 176 en la parte izquierda y calculamos la resta 215-176:
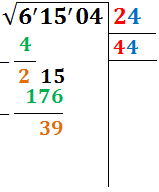
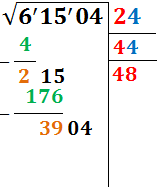
En la derecha, en un nuevo renglón, bajamos el doble del primer renglón. Es decir, escribimos 48 en un nuevo renglón.
En la izquierda, bajamos el siguiente par, es decir, 04.
-
Repetimos los pasos anteriores hasta que no haya más pares para bajar:
Buscamos un número x para que al añadirlo a la derecha del renglón inferior y multiplicar este número por x, se aproxime al número de la parte izquierda (por debajo):

El número que más se aproxima a 3904 (por debajo) es 3904. Este número es el resultado del producto 448·8.
Por tanto, escribimos 8 en la parte derecha (en el primer y en el último renglón):
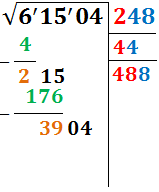
Escribimos el resultado del producto, 3904, en la parte izquierda y calculamos la resta 3904-3904:
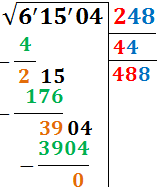
Como el resto obtenido es 0, el proceso ha terminado y la raíz de 61504 es un número entero (el del primer renglón de la derecha): 248.
Por tanto,
√61504 = 248
Enlace: Cálculo de raíces cuadradas (con y sin decimales).
Ecuaciones Resueltas:
- Nivel 1: primeras ecuaciones
- Nivel 2: número de soluciones
- Nivel 3: ecuaciones con paréntesis
- Nivel 4: ecuaciones con fracciones
- Nivel 5: ecuaciones con fracciones y con paréntesis
- Nivel 6: 50 problemas resueltos
Otros:
- Fracciones equivalentes e irreductibles
- Potencias
- Ecuaciones de primer grado
- Problemas con ecuaciones de primer grado
- Problemas de sistemas de ecuaciones
- Ecuaciones de segundo grado
- Problemas de Pitágoras
- Progresiones
- Ecuaciones exponenciales


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


