RECURSOS DE APRENDIZAJE
-
Presentación 2 Room.pdf

Presentación 2 Educación Física
Área de conocimientoContexto educativoTipo de recursoColecciones -
Límites laterales y continuidad: II. Límite por la derecha
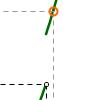
En esta actividad veremos qué significado tiene el límite por la derecha de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.
Área de conocimientoTipo de recursoColecciones -
Billar
En esta actividad mediante el juego del billar se practican diversos ejemplos de simetrías axiales.
Área de conocimientoTipo de recursoColecciones -
Límites laterales y continuidad: I. Límite por la izquierda
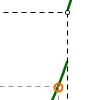
En esta actividad veremos qué significado tiene el límite por la izquierda de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.
Área de conocimientoTipo de recursoColecciones -
Lados curvos

El objetivo en esta actividad es averiguar cómo se forman figuras complejas alterando algunos elementos de figuras sencillas, como polígonos regulares y circunferencias.
Área de conocimientoTipo de recursoColecciones -
Simetría rotacional

En esta actividad se practica con simetrías rotacionales. Decimos que una figura plana tiene simetría rotacional cuando podemos encontrar un centro (llamado centro de rotación) de manera que si giramos la figura completa un cierto ángulo (mayor o igual a 0º y menor que 360º), la figura rotada coincide con la figura original. Cuando un figura tiene simetría rotacional, a cada punto le corresponden otro punto (que se llama "punto rotado" o "imagen") a la misma distancia del centro, de forma que...
Área de conocimientoTipo de recursoColecciones -
Tamaño aparente de la luna y del sol

Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta actividad podrás comprobar cómo con la simple observación directa, sin sofisticados instrumentos, Aristarco consiguió medir el tamaño aparente de la Luna y Sol en el cielo, es decir, determinar el valor del ángulo con el que los vemos.
Área de conocimientoTipo de recursoColecciones -
Calculadora de límites de funciones
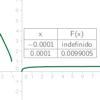
La forma más sencilla de averiguar aproximadamente a qué valor se aproxima una función F cuando x se acerca a un valor determinado c, consiste simplemente en averiguar el valor de la función para valores muy próximos a c, como F(c + 0.0001) o como F(c - 0.0001). Pero a veces el cálculo del límite es solo una operación intermedia, por lo que necesitamos valores exactos, no aproximados. Esta actividad es una herramienta útil para el cálculo de límites de funciones.
Área de conocimientoTipo de recursoColecciones -
Límites laterales y continuidad: III. Continuidad
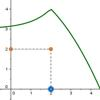
En esta actividad veremos qué significado tiene el límite de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.
Área de conocimientoTipo de recursoColecciones -
Espirales

Se trata de utilizar una construcción de Geogebra en la que aparecen figuras reales, piñas y girasoles, y sobre ellas se dibujan espirales y se cuenta el número de espirales en uno u otro sentido, observando que coincide siempre con dos términos consecutivos de la sucesión de Fibonacci.
Área de conocimientoTipo de recursoColecciones -
Copa

Solemos infravalorar la longitud de la circunferencia, pues tomamos como referencia el diámetro, olvidándonos que la longitud real es aproximadamente 3 veces ( pi veces) el diámetro. Objeto digital educativo que formula cuestiones relacionadas con el diámetro de la circunferencia descrita por el borde de una copa y la altura de esta. La aplicación incluye autoevaluación.
Tipo de recursoColecciones -
Criba de Eratóstenes

Profundización en el concepto de divisibilidad y clasificación de números enteros usando métodos tradicionales de forma dinámica, interactiva e intuitiva, adquiriendo de forma directa el concepto de número entero compuesto y primo, y afianzando el uso de las operaciones con números enteros.
Área de conocimientoTipo de recursoColecciones -
Cuentas con cuentas (de 6 en 6)
Profundización en las operaciones con números enteros y en los conceptos de múltiplo, divisor, cociente y resto. Así mismo se introducen técnicas para el estudio de la combinatoria y las regularidades numéricas de una forma lúdica, interactiva e intuitiva.
Área de conocimientoTipo de recursoColecciones -
Cuentas con cuentas (de 4 en 4)
Profundización en las operaciones con números enteros y en los conceptos de múltiplo, divisor, cociente y resto. Así mismo se introducen técnicas para el estudio de la combinatoria y las regularidades numéricas de una forma lúdica, interactiva e intuitiva.
Área de conocimientoTipo de recursoColecciones -
Primos gemelos
Profundización en el concepto de divisibilidad y clasificación de números enteros en concreto se estudian ciertas propiedades de los números primos.
Tipo de recursoColecciones -
Polígonos estrellados

Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Si dividimos la circunferencia en arcos de igual longitud, al unir los extremos consecutivos de esos arcos obtendremos polígonos regulares con esos vértices: triángulos equiláteros, cuadrados, pentágonos regulares, etc., pero si en vez de unir vértices consecutivos (es decir, en vez de "saltar" de uno en ...
Área de conocimientoTipo de recursoColecciones -
Regulares anidados

Este es uno de los objetos educativos del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra, esta aplicación representa varias situaciones geométricas facilitando la observación de sus propiedades y las regularidades que se repiten en ellas, lo que permite al usuario, después de analizar detenidamente la situación, elaborar una fórmula que ponga de manifiesto dichas regularidades.
Área de conocimientoTipo de recursoColecciones -
Talleres 5

Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Talleres 5 es la quinta de 5 actividades que nos introducen en el manejo de Geogebra. En estos talleres te proponemos una serie de objetivos, gradualmente más complejos, que debes intentar realizar. Muchas veces hay distintas formas de lograrlo, por eso en estos talleres las preguntas no te van a ofrecer apenas pistas, debes ser tú quien explore...
Área de conocimientoTipo de recursoColecciones -
Talleres 3

Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Talleres 3 es la tercera de 5 actividades que nos introducen en el manejo de Geogebra. En estos talleres te proponemos una serie de objetivos, gradualmente más complejos, que debes intentar realizar. Muchas veces hay distintas formas de lograrlo, por eso en estos talleres las preguntas no te van a ofrecer apenas pistas, debes ser tú quien explor...
Área de conocimientoTipo de recursoColecciones -
Semáforo de banderas

Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Simplemente por la posición de los brazos podemos establecer un sistema de comunicación entre personas algo distantes. Cada posición de los brazos corresponde con una letra del alfabeto. En la aplicación puedes ver esa relación. Podrás asociar el lenguaje con los ángulos que forman los brazos.
Área de conocimientoTipo de recursoColecciones


