Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 7 (*2222, pmm). Es el tercero de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de rectángulo.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 6 (xx, pg). Es el segundo de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de rectángulo.

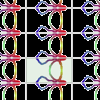Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 5 (**, pm). Es el primero de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de rectángulo.

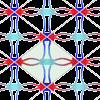Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 4 (2*22, cmm). Es el segundo de los dos grupos de mosaicos que se pueden crear con azulejos con forma de rombo.

En la escena se pueden observar y manipular ejemplos de los cuatro tipos de isometrías y conocer sus principales características: Traslación, Rotación o Giro, Reflexión o Simetría axial y Reflexión Desplazada.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 3 (*x, cm). Es el primero de los dos grupos de mosaicos que se pueden crear con azulejos con forma de rombo.

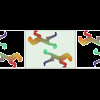Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 3. Es el último de los tres grupos de frisos que se pueden crear sin ninguna simetría axial (reflexión). Corresponde a huellas de un mismo pie, en la ida y en la vuelta.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 1 2 (2222, p2). Es el segundo de los dos grupos de mosaicos que se pueden crear con azulejos con forma de romboide.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta primera actividad se explora el grupo 1 (o, p1). Es un grupo especial y muy sencillo: simplemente no se hacen copias del motivo decorativo dentro del mismo azulejo. En el azulejo se dibuja cualquier cosa que no tenga simetría, de este modo, las únicas sime...

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Esta actividad permite practicar la búsqueda del grupo de isometrías correspondiente a un friso cualquiera. Es aconsejable realizar primero prácticas del uso del explorador (se puede hacer pulsando el enlace correspondiente).

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Esta actividad permite practicar el procedimiento para averiguar a qué grupo de isometrías corresponde un friso cualquiera.

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Esta actividad permite practicar la búsqueda del grupo de isometrías correspondiente a un friso cualquiera. Es aconsejable realizar primero prácticas del uso del explorador.

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. En esta actividad se puede crear un diseño propio de un friso. Para ello primero hay que elegir el grupo de isometrías, situar los vértices del azulejo que se repite por traslación y dibujar el motivo decorativo en la región sombreada.

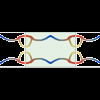Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad explorarás el grupo 7. Es el último de los cuatro grupos de frisos que se pueden crear usando algún espejo. Corresponde a una ida y vuelta de saltos.

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad explorarás el grupo 6. Es el tercero de los cuatro grupos de frisos que se pueden crear usando algún espejo. Corresponde al movimiento ladino, en ida y vuelta.

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 5. Es el segundo de los cuatro grupos de frisos que se pueden crear usando algún espejo. Corresponde a andar de lado, como a hurtadillas, de forma ladina.

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 4. Es el primero de los cuatro grupos de frisos que se pueden crear usando algún espejo. Corresponde a marcas de saltos con ambos pies.

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 2. Es el segundo de los tres grupos de frisos que se pueden crear sin ninguna simetría axial (reflexión). Corresponde a las marcas de los pasos al caminar.

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los frisos a la que se puede acceder desde la misma página. En esta actividad se explora el grupo 1. Es un grupo especial y muy sencillo: simplemente no se hacen copias del motivo decorativo dentro del mismo azulejo.

Cuando giramos una figura plana (como un polígono, por ejemplo) alrededor de una recta (llamada eje de revolución) obtenemos un "cuerpo de revolución". En esta aplicación vamos a crear cuerpos de revolución de una forma muy similar al modo en que el alfarero emplea el torno para realizar obras de cerámica. Incluye las soluciones a las actividades propuestas.