PROCOMÚN
Emaitzak erakusten 501 520 565 guztira
-
Dos progresiones aritméticas sobre objetos geométricos
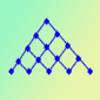 En las siguientes actividades se trata de relacionar el número de segementos o de cuadrados de una figura con la posición que ocupa esta en la serie que se visualiza. La relación podrá escribirse mediante una expresión algebraica que será la ley de formación de la sucesión.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
En las siguientes actividades se trata de relacionar el número de segementos o de cuadrados de una figura con la posición que ocupa esta en la serie que se visualiza. La relación podrá escribirse mediante una expresión algebraica que será la ley de formación de la sucesión.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Descomposición del cubo
 Mediante esta escena se deduce la fórmula del volumen de una pirámide a partir del volumen de un cubo mediante descomposición del mismo.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
Mediante esta escena se deduce la fórmula del volumen de una pirámide a partir del volumen de un cubo mediante descomposición del mismo.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Desarrollo del tetraedro
 DESARROLLO DE POLIEDROS Si en un poliedro, o en un cuerpo de revolución, cortamos por un número suficiente de aristas, o generatrices y bordes, de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro, o cuerpo de revolución. En el supuesto que hayas realizado esta práctica manualmente, habrás podido comprobar que, partiendo de un desarrollo del poliedro, o cuerpo de revolución, es más sencillo construirlos. La escena muestra, paso a paso, el desarro...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
DESARROLLO DE POLIEDROS Si en un poliedro, o en un cuerpo de revolución, cortamos por un número suficiente de aristas, o generatrices y bordes, de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro, o cuerpo de revolución. En el supuesto que hayas realizado esta práctica manualmente, habrás podido comprobar que, partiendo de un desarrollo del poliedro, o cuerpo de revolución, es más sencillo construirlos. La escena muestra, paso a paso, el desarro...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Desarrollo del prisma pentagonal regular
 DESARROLLO DE POLIEDROS Y CUERPOS DE REVOLUCIÓN: Si en un poliedro, o en un cuerpo de revolución, cortamos por un número suficiente de aristas, o generatrices y bordes, de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro, o cuerpo de revolución. En el supuesto que hayas realizado esta práctica manualmente, habrás podido comprobar que, partiendo de un desarrollo del poliedro, o cuerpo de revolución, es más sencillo construirlos. La escena muestr...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
DESARROLLO DE POLIEDROS Y CUERPOS DE REVOLUCIÓN: Si en un poliedro, o en un cuerpo de revolución, cortamos por un número suficiente de aristas, o generatrices y bordes, de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro, o cuerpo de revolución. En el supuesto que hayas realizado esta práctica manualmente, habrás podido comprobar que, partiendo de un desarrollo del poliedro, o cuerpo de revolución, es más sencillo construirlos. La escena muestr...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Desarrollo del ortoedro
 DESARROLLO DE POLIEDROS Si en un poliedro, o en un cuerpo de revolución, cortamos por un número suficiente de aristas, o generatrices y bordes, de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro, o cuerpo de revolución. En el supuesto que hayas realizado esta práctica manualmente, habrás podido comprobar que, partiendo de un desarrollo del poliedro, o cuerpo de revolución, es más sencillo construirlos. La escena muestra, paso a paso, el desarro...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
DESARROLLO DE POLIEDROS Si en un poliedro, o en un cuerpo de revolución, cortamos por un número suficiente de aristas, o generatrices y bordes, de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro, o cuerpo de revolución. En el supuesto que hayas realizado esta práctica manualmente, habrás podido comprobar que, partiendo de un desarrollo del poliedro, o cuerpo de revolución, es más sencillo construirlos. La escena muestra, paso a paso, el desarro...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Desarrollo del cubo
 DESARROLLO DE POLIEDROS Si en un poliedro, o en un cuerpo de revolución, cortamos por un número suficiente de aristas, o generatrices y bordes, de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro, o cuerpo de revolución. En el supuesto que hayas realizado esta práctica manualmente, habrás podido comprobar que, partiendo de un desarrollo del poliedro, o cuerpo de revolución, es más sencillo construirlos. La escena muestra, paso a paso, el desarro...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
DESARROLLO DE POLIEDROS Si en un poliedro, o en un cuerpo de revolución, cortamos por un número suficiente de aristas, o generatrices y bordes, de forma que quede una sola pieza y la extendemos en el plano, obtenemos un desarrollo del poliedro, o cuerpo de revolución. En el supuesto que hayas realizado esta práctica manualmente, habrás podido comprobar que, partiendo de un desarrollo del poliedro, o cuerpo de revolución, es más sencillo construirlos. La escena muestra, paso a paso, el desarro...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Del tetraedro al octaedro
 De las infinitas formas de truncar un tetraedro, que podemos ver con esta escena, hay dos que producen resultados singulares: el tetraedro truncado y el octaedro.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
De las infinitas formas de truncar un tetraedro, que podemos ver con esta escena, hay dos que producen resultados singulares: el tetraedro truncado y el octaedro.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Construir un trángulo conocidos dos ángulos y un lado
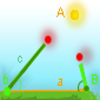 Construcción dinámica e interactiva de un triángulo, conocidos dos ángulos y un lado.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
Construcción dinámica e interactiva de un triángulo, conocidos dos ángulos y un lado.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Constructor de poliedros
 Con esta escena se podrán crear, manipular y visualizar distintos tipos de poliedros.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
Con esta escena se podrán crear, manipular y visualizar distintos tipos de poliedros.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Aproximaciones por defecto y por exceso del número PI. Método de Arquímedes
 En este Ode de forma interactiva se realiza una aproximación al número Pi a través de la circunferencia inscrita y circunscrita en diferentes polígonos regulares.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
En este Ode de forma interactiva se realiza una aproximación al número Pi a través de la circunferencia inscrita y circunscrita en diferentes polígonos regulares.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Límites de sucesiones
 Ejercicios relacionados con diversos tipos de límites que en principio corresponden a la indeterminada infinito menos infinito, y que se resuelven a través de la técnica de los conjugados.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
Ejercicios relacionados con diversos tipos de límites que en principio corresponden a la indeterminada infinito menos infinito, y que se resuelven a través de la técnica de los conjugados.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Laberinto con suma de enteros
 Se propone un juego en el que se tiene que atravesar un tablero siguiendo la trayectoria elegida, según la cual se van sumando los puntos correspondientes a las casilas por las que se pasa. El tiempo es ilimitado, solo se tiene la limitación del valor máximo impuesto.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
Se propone un juego en el que se tiene que atravesar un tablero siguiendo la trayectoria elegida, según la cual se van sumando los puntos correspondientes a las casilas por las que se pasa. El tiempo es ilimitado, solo se tiene la limitación del valor máximo impuesto.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
La raíz cuadrada de un número natural: animación
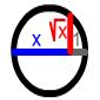 La forma más habitual de representar las raices cuadradas de los números naturales es mediante una figura que recibe el nombre de Caracol Pitagórico, que se basa en la utilización del teorema de Pitágoras. En esta animación se puede ver otra forma de representarlas. Se visualiza en primer lugar la representación gráfica de la raíz cuadrada de un número real utilizando para ello el teorema de la altura. Después se representan las raíces los números naturales del 1 hasta el 6. Uniendo los punto...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
La forma más habitual de representar las raices cuadradas de los números naturales es mediante una figura que recibe el nombre de Caracol Pitagórico, que se basa en la utilización del teorema de Pitágoras. En esta animación se puede ver otra forma de representarlas. Se visualiza en primer lugar la representación gráfica de la raíz cuadrada de un número real utilizando para ello el teorema de la altura. Después se representan las raíces los números naturales del 1 hasta el 6. Uniendo los punto...Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Interpretación geométrica de la derivada direccional
 applet Descartes que permite de forma gráfica visualizar los conceptos de tangentes en superficies. Trabaja con los términos de derivadas parciales. Sus controles permiten modificar las condiciones iniciales.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
applet Descartes que permite de forma gráfica visualizar los conceptos de tangentes en superficies. Trabaja con los términos de derivadas parciales. Sus controles permiten modificar las condiciones iniciales.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Integrales por sustitución
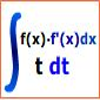 Applet Descartes con catorce tipos de ejercicios ( con sus soluciones) sobre integrales que se resuelven mediante el método de sustitución.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
Applet Descartes con catorce tipos de ejercicios ( con sus soluciones) sobre integrales que se resuelven mediante el método de sustitución.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Hipérbola reglada
 La escena muestra, paso a paso, la manera en que al mover el punto P alrededor de la circunferencia, las sucesivas mediatrices del segmento PQ, van perfilando una hipérbola.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
La escena muestra, paso a paso, la manera en que al mover el punto P alrededor de la circunferencia, las sucesivas mediatrices del segmento PQ, van perfilando una hipérbola.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Giros de un triángulo en el plano
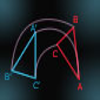 Escena dinámica e interactiva para efectuar y observar los giros de un triángulo en el plano.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
Escena dinámica e interactiva para efectuar y observar los giros de un triángulo en el plano.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Funciones trigonométricas e hiperbólicas
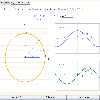 La funciones trigonométricas e hiperbólicas están asociadas a unas curvas, circunferencia e hipérbola. En la escena se expone dicha relación de forma clara, de esta forma pretendemos una mejor comprensión de dichas funciones.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
La funciones trigonométricas e hiperbólicas están asociadas a unas curvas, circunferencia e hipérbola. En la escena se expone dicha relación de forma clara, de esta forma pretendemos una mejor comprensión de dichas funciones.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Funciones definidas a trozos
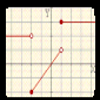 En esta escena Descartes se puede practicar la representación gráfica de funciones definidas en varios trozos de recta o funciones polinómicas de primer grado. También se presta atención a algunas de sus propiedades, dominio, crecimiento o decrecimiento, recorrido, etc..Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
En esta escena Descartes se puede practicar la representación gráfica de funciones definidas en varios trozos de recta o funciones polinómicas de primer grado. También se presta atención a algunas de sus propiedades, dominio, crecimiento o decrecimiento, recorrido, etc..Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones -
Factorial de un número
 En esta escena puedes calcular el factorial de un número con todas sus cifras. Por razones de visualización el factorial máximo que puedes calcular es el de 1000.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones
En esta escena puedes calcular el factorial de un número con todas sus cifras. Por razones de visualización el factorial máximo que puedes calcular es el de 1000.Jakintza-arloHezkuntza-testuinguruaBaliabide motaColecciones


