Movimiento Rectilíneo Uniforme
Movimiento Rectilíneo Uniforme
El movimiento es rectilíneo uniforme cuando la trayectoria es una línea recta y la velocidad es constante (no existe aceleración).
En este movimiento, la distancia recorrida, x, es proporcional al tiempo, t, y a la velocidad, v:
x = v·t
Por tanto, cuanto más tiempo dure el desplazamiento o cuanto mayor sea la velocidad, mayor es la distancia recorrida.
1. Datos iniciales
Si el movimiento comienza en la posición x0 y en el tiempo t0, entonces la posición del móvil en el instante t es
x = x0 + v·(t - t0)
2. Gráfica de la distancia en función del tiempo
Como la distancia recorrida es proporcional al tiempo, la gráfica de la distancia en función del tiempo es una recta.
La siguiente gráfica muestra el espacio recorrido por dos movimientos rectilíneos uniformes: el del móvil A, con velocidad 5km/h; y el del móvil B, con velocidad 7km/h.
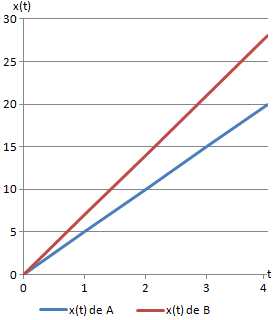
Si la gráfica x(t) no es una recta, el movimiento no es rectilíneo uniforme.
3. Problema 1
La velocidad de la luz en el vacío es c = 300 000 km/s. La luz del Sol tarda en llegar a la Tierra 8 minutos y 19 segundos. Calcular la distancia entre el Sol y la Tierra.
Solución:
La velocidad la hemos llamado c en vez de v ya que para la luz se utiliza este nombre. Por tanto, conocemos la velocidad, c, y el tiempo, t = 8 min 19s. Podemos calcular la distancia:
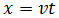
Antes de sustituir tenemos que expresar el tiempo en una sola unidad. Como la velocidad la tenemos en kilómetros por segundo, pasamos el tiempo a segundos:
Por un lado, los 8 minutos son
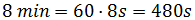
Por tanto, el tiempo es
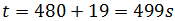
Ahora sustituimos los datos en la ecuación:
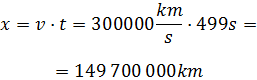
Por tanto, la distancia del Sol a la Tierra es de 149 700 000km, es decir, casi 150 millones de kilómetros.
4. Problema 2
En el mismo instante, una motocicleta sale de la ciudad A y otra de la ciudad B, con la intención de encontrarse en el camino recto de 60 kilómetros que une ambas ciudades.
Sabiendo que las velocidades de las motocicletas son 70km/h y 55km/h, calcular cuánto tardarán en encontrarse.
Solución:
El diagrama de la situación es
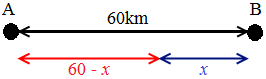
Como cada motocicleta circula a una velocidad, no se encuentran en la mitad del camino. La que tiene una velocidad menor habrá recorrido x kilómetros y, por tanto, la otra habrá recorrido 60-x, ya que la suma de ambas distancias ha de ser la distancia que hay entre las ciudades. En efecto,
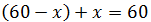
Por otro lado, el tiempo es el mismo para ambas motocicletas ya que salen en el mismo instante.
La ecuación del movimiento rectilíneo uniforme es
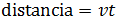
Para la motocicleta que circula a 55km/h tenemos
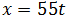
Y, para la otra
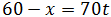
Tenemos un sistema de ecuaciones:
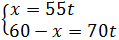
Sustituimos la primera ecuación en la segunda:
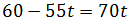
Resolvemos la ecuación de primer grado:
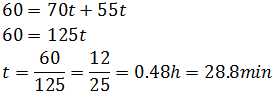
Por tanto, las motocicletas se encuentran transcurridos unos 29 minutos desde su salida.
Enlaces:
Ecuaciones Resueltas:
- Nivel 1: primeras ecuaciones
- Nivel 2: número de soluciones
- Nivel 3: ecuaciones con paréntesis
- Nivel 4: ecuaciones con fracciones
- Nivel 5: ecuaciones con fracciones y con paréntesis
- Nivel 6: 50 problemas resueltos
Otros:
- Fracciones equivalentes e irreductibles
- Potencias
- Ecuaciones de primer grado
- Problemas con ecuaciones de primer grado
- Problemas de sistemas de ecuaciones
- Ecuaciones de segundo grado
- Problemas de Pitágoras
- Progresiones
- Ecuaciones exponenciales

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.



