Ecuaciones Exponenciales
Ecuaciones Exponenciales
Una ecuación exponencial es aquella en la que aparecen exponenciales, es decir, potencias cuyos exponentes son expresiones en las que aparece la incógnita, x. En esta sección, resolveremos ecuaciones exponenciales sin usar logaritmos.
El método de resolución consiste en conseguir una igualdad de exponenciales con la misma base para poder igualar los exponentes. Para ello, utilizaremos las propiedades de las potencias.
Ejemplo 1:
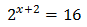
Escribimos 16 como una potencia de 2:
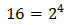
Podemos reescribir la ecuación como
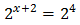
Por tanto, igualando los exponentes,
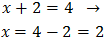
Luego la solución de la ecuación exponencial es x = 2.
Ejemplo 2:
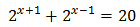
Aplicando las propiedades de las potencias,
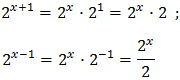
Con lo que podemos reescribir la ecuación como
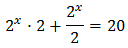
De este modo podemos extraer factor común:
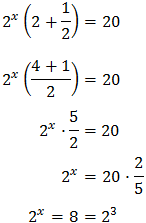
Es decir, la solución es x = 3.
Ejemplo 3:
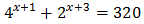
Las bases de las exponenciales son distintas, pero ambas son potencias de 2. Operamos para tener potencias con la misma base:
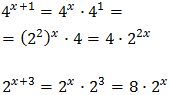
Con lo que podemos reescribir la ecuación como

Aplicamos un cambio de variable:
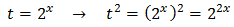
Substituimos en la ecuación y obtenemos la ecuación de segundo grado
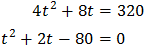
cuyas soluciones son
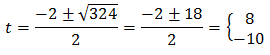
Por tanto,
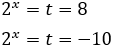
La segunda solución no es posible por ser negtiva. Por tanto,
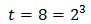
Es decir, debe cumplirse
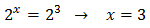
La única solución de la ecuación exponencial es x = 3.
Más información:
Ecuaciones Resueltas:
- Nivel 1: primeras ecuaciones
- Nivel 2: número de soluciones
- Nivel 3: ecuaciones con paréntesis
- Nivel 4: ecuaciones con fracciones
- Nivel 5: ecuaciones con fracciones y con paréntesis
- Nivel 6: 50 problemas resueltos
Otros:
- Fracciones equivalentes e irreductibles
- Potencias
- Ecuaciones de primer grado
- Problemas con ecuaciones de primer grado
- Problemas de sistemas de ecuaciones
- Ecuaciones de segundo grado
- Problemas de Pitágoras
- Progresiones
- Ecuaciones exponenciales


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


