El alumnado deberá trabajar diferentes contenidos, a lo largo de varias sesiones, sobre la plataforma de geometría dinámica Geogebra. Desde cero, deberán ir haciendo diferentes prácticas hasta conseguir hacer una propia aplicación interactiva donde puedan explicar la resolución de un sistema de ecuaciones de forma gráfica. Usando variables y visualización condicional. Está enfocado para la asignatura de matemáticas en segundo de la ESO, para un perfil que no haya trabajado demasiado con Geoge...

“¡A representar! Resolviendo ecuaciones para diseñar una ciudad matemática” El alumnado trabajará en parejas para resolver ecuaciones de primer grado con una incógnita. A partir de los resultados obtenidos, representarán gráficamente las soluciones en el plano cartesiano, creando una "ciudad matemática", donde cada ecuación representará un edificio, una calle o un elemento del entorno. El producto final será una presentación digital o infografía que incluya el trabajo realizado, con explicac...

Con este recurso, se pretende iniciar al alumno en la multiplicación: su definición, procedimiento, además de unos ejercicios prácticos. También cuenta con la explicación del procedimiento.

Situación de aprendizaje con la que se persigue que el alumnado, de forma divertida, utilice los porcentajes en situaciones de la vida cotidiana, así como tenga una primera toma de contacto con las empresas, creando una empresa ficticia con su logotipo y su folleto de artículos.

Calendario curso 24-25 con operaciones matemáticas.

Estudiar la biografía de una mujer científica, resumirla y exponerla. Mujeres Matemáticas y Científicas © 2025 by José Antonio Alenda is licensed under CC BY-NC 4.0 

Las ecuaciones son herramientas versátiles y poderosas en diferentes campos y situaciones de la vida diaria, nos ayudan a resolver problemas del día a día, desde calcular gastos hasta diseñar edificios. Los alumnos nos preguntan muchas veces a que sirven. Con esta actividad descubrirán por si solo el uso de las ecuaciones.

Estudi de les funcions exponencials i logaritmiques

Este recurso va dirigido al alumnado de Infantil donde podréis trabajar las funciones ejecutivas, la atención visual y la concentración, orientación espacial, discriminación visual, coordinación óculo-manual y motricidad fina, e incluso también encarado a trabajar habilidades como la imitación, el aprendizaje por observación, la autonomía o la estructuración cognitiva.  En el mismo PDF tenéis con más detalle la explicación de qué podemos trabajar con este, así como también el material en sí ...

Situació d'aprenentage per a ESO de geometria

En esta actividad el alumnado trabajará el concepto de porcentaje. Para ello deberá crear un negocio e ir calculando porcentajes en la factura realizada con los productos o actividades ofertados.

Situación de aprendizaje para 1º de la ESO sobre estadística

La elección de esta SdA está basada en lo que saqué en claro de la rutina de pensamiento que hice antes. Me di cuenta de que trabajar la estadística de forma práctica, usando herramientas como hojas de cálculo, ayudaba mucho a que los alumnos estuvieran más motivados y participaran más. Eso sí, también vi que había cosas que mejorar, como organizar mejor el uso de la tecnología y prestar más atención a los alumnos que tenían más problemas para adaptarse a estas herramientas. Por eso, este ...

Análisis en el aula de la importancia de las mujeres en la ciencia y en las matemáticas.

RESOLUCIÓN PROBLEMAS DESAYUNO ANDALUZ

Que los alumnos aprenda a usar fracciones

Situación de Aprendizaje de Áreas y Perímetros.

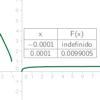
La forma más sencilla de averiguar aproximadamente a qué valor se aproxima una función F cuando x se acerca a un valor determinado c, consiste simplemente en averiguar el valor de la función para valores muy próximos a c, como F(c + 0.0001) o como F(c - 0.0001). Pero a veces el cálculo del límite es solo una operación intermedia, por lo que necesitamos valores exactos, no aproximados. Esta actividad es una herramienta útil para el cálculo de límites de funciones.

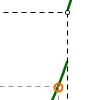
En esta actividad veremos qué significado tiene el límite por la izquierda de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.

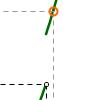
En esta actividad veremos qué significado tiene el límite por la derecha de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.