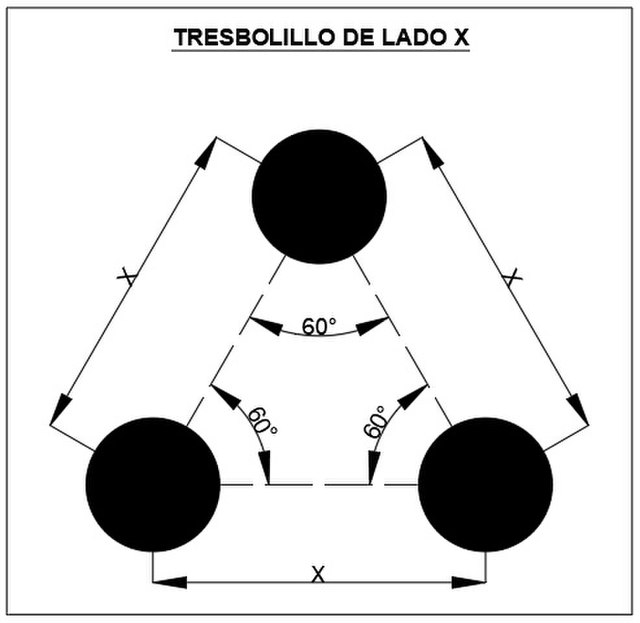Hoja de cálculo Excel para determinar el número de plantas que caben en una parcela con una superficie determinada atendiendo al marco de plantación.

Primera unidad del módulo Operaciones Auxiliares de Gestión de Tesorería del segundo curso del ciclo formativo de grado medio de Gestión Administrativa. Los contenidos que se van a trabajar en esta tarea van a contribuir a alcanzar el resultado de aprendizaje 3 (criterios de evaluación a) y d)) y resultado de aprendizaje 4 (criterio de evaluación h)).

Esta situación de aprendizaje está diseñada para trabajar los saberes básicos de matemática financiera en 1º de Grado medio de FP Administrativo. Se introducen los conceptos de la matemática financiera: interés simple y compuesto así como la simulación de la amortización de un préstamo y se recuerdan porcentajes y variaciones porcentuales, como herramientas para el entendimiento y compresión de las elecciones de la empresa en la búsqueda de Financiación Ajena a Largo plazo.

Proyecto sobre la aplicación de herramientas digitales para desenvolverse en la vida adulta, aplicable desde el nivel de 3ºESO en adelante, para trabajar la competencia digital y la motivación del alumnado.

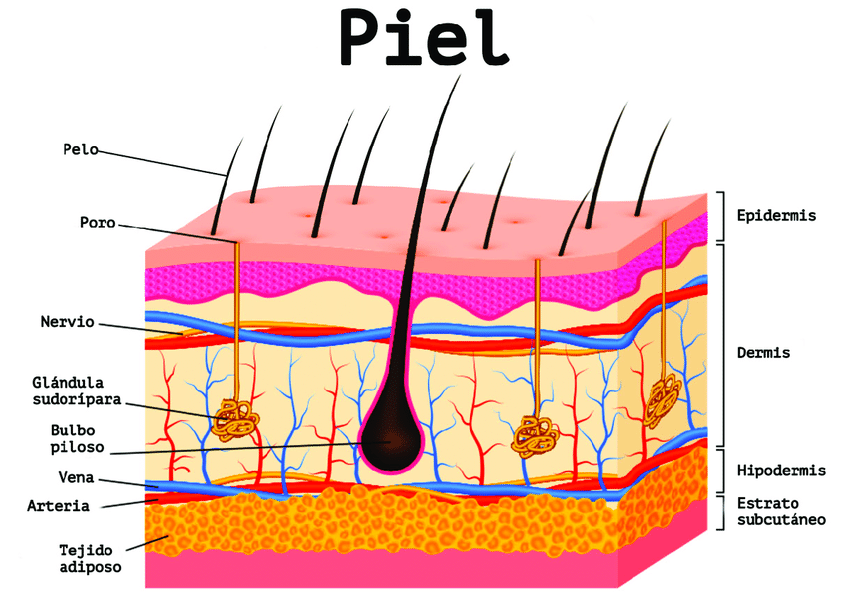La piel es la cubierta externa de los animales vertebrados y uno de sus órganos más importantes. Actúa como una barrera protectora que aísla al organismo del medio que lo rodea, protegiéndolo y contribuyendo a mantener íntegras sus estructuras. Además, funciona como un sistema de comunicación con el entorno y es uno de los principales órganos sensoriales.

Las siguientes actividades se encuadran dentro de la asignatura de Técnicas Básicas de Enfermería de primer curso del CFGM de Auxiliar de Enfermería, en las que el alumnado aprenderá la utilidad de las matemáticas aplicas a la farmacología. A través de ejemplos prácticos y cotidianos, se introducirán conceptos básicos de la posología y sus sus variaciones en función de edad, peso, efectos secundarios, etc.

Collage utilizando la aplicación "KD Collage", en donde cada foto deberá incluir un QR generado por la aplicación "Unitage" y lo entregará en formato pdf, adjuntado a la tarea propuesta en "Classroom". Cada QR hará referencia a una figura geométrica plana o espacial, simple o compuesta, expresando sus dimensiones, en la que se pretenda calcular el área de la figura plana o el volumen en el caso de figura espacial (cuerpo geométrico), evaluando las posibles soluciones que pueden darse relacion...

Os presento en el siguiente enlace el trabajo de centro con 12 lesson plans elaboradas por el equipo SymbalooEDU del colegio, 12 compañeros que hemos cursado “Aprendizaje personalizado en entornos digitales”. URL: Webmix-Colegio La Merced-Jesuitas-Burgos Centro educativo: La Merced y San Francisco Javier”. Jesuitas. Burgos. El boceto de centro se diseñó siguiendo un mismo hilo conductor en el centro: “El comercio”. De esta forma, los contenidos que se trabajan en los itinerarios giran en...

Movimiento Rectilíneo Uniforme El movimiento es rectilíneo uniforme cuando la trayectoria es una línea recta y la velocidad es constante (no existe aceleración). En este movimiento, la distancia recorrida, x, es proporcional al tiempo, t, y a la velocidad, v: x = v·t Por tanto, cuanto más tiempo dure el desplazamiento o cuanto mayor sea la velocidad, mayor es la distancia recorrida. 1. Datos iniciales Si el movimiento comienza en la posición x0 y en el tiempo t0, entonces la posición ...

Equacions exponencials i logarítmiques 1. Equacions exponencials Una equació exponencial és aquella en la que apareixen exponencials, és a dir, potències que tenen la incògnita, x, en els exponents. En aquesta pàgina resoldrem equacions exponencials sense emprar logaritmes. El mètode de resolució consisteix en aconseguir una igualtat entre dues exponencials amb la mateixa base per poder igualar els seus exponents. Aplicarem les propietats de les potències. Exemple 1: Si escrivim 27 com...

Equacions de segon grau completes i incompletes Una equació de segon grau és una equació polinòmica de grau 2, és a dir, el major grau dels monomis és 2, o siga, x al quadrat. Com que l'equació és de grau 2, tindrà, com a molt, dues arrels (solucions) distintes. Tota equació de segon grau es pot escriure en la forma Si ningun dels coeficients, a,b i c és zero, és a dir, direm que l'equació és completa. Si no és així (si b ó c és 0), direm que és incompleta. 1. Equació completa Les...

Si conocemos dos lados de un triángulo rectángulo, podemos calcular el otro lado aplicando el teorema de Pitágoras. Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno. El coseno de un ángulo α se define como el cociente del lado contiguo al ángulo α y la hipotenusa. De forma análoga, el seno de α se define como el cociente del lado opuesto al ángulo α y la hipotenusa. Nota: si...

Intervalos Definimos el intervalo [a,b] siendo a<b como el conjunto formado por todos los números (reales) que son mayores o iguales que a y menores o iguales que b. Los números a y b se denominan extremos del intervalo [a,b]. Representación en la recta real del intervalo [a,b]: Ejemplos: El número 3 está en el intervalo [0,5] porque 3 es mayor o igual que 0 y menor o igual que 5. El número 6 no está en el intervalo [0,5] porque es mayor o igual que 0 pero no es menor o ...

Hola, en el siguiente enlace pueden encontrar ejercicios interactivos de matemáticas. Son ejercicios con auto-corrección de álgebra, operaciones entre enteros, tablas de multiplicar.... Además, en la misma web Matesfacil.com, pueden encontrar apuntes y problemas resueltos de matemáticas para secundaria y bachillerato. Un saludo. Enlace: Ejercicios interactivos Otros: Problemas y Ecuaciones Ecuaciones Resueltas

Cálculo de Ráices Cuadradas Vamos a ver las partes de una raíz cuadrada y el algoritmo (método) para calcular la raíz cuadrada de un número. Partes de una raíz cuadrada: El radicando es el número cuya raíz queremos calcular. Es decir, si b es el radicando y aes la raíz de b, entonces a al cuadrado es b. El radicando se escribe bajo el signo radical. Por ejemplo, si el radicando es 4, entonces la raíz cuadrada es 2 ya que 2 al cuadrado es 4. Si la raíz cuadrada no es número exacto (o se...

Pythagoren Theorem Pythagoras' Theorem: Given a right triangle with sides a and b and a hypotenuse h (the side opposite the right angle). Then, Remember that... triangle is a right-angled triangle because it has a right angle, an angle of 90º or π / 2 radians The hypotenuse is the opposite side as the right angle. Note: h is always bigger than the other sides, as shows h > a and h > b. The Pythagoras theorem is one of the most known results in mathematics and also one...

1. Definición Informalmente, seafuna función biyectiva. Entonces, su función inversa,g,es la función que proporciona las anti-imágenes del recorrido def. Por ejemplo, sif(a) = b, entoncesg(b) = a. Ejemplo: La inversa de la funciónf(x) = 2xesg(x) = x/2. Veamos quegproporciona las anti-imágenes def: f(2) = 2·2 = 4, g(4) = 4/2 = 2 f(3) = 2·3 = 6, g(6) = 6/2 = 3 f(-10) = 2·(-10) = -20, g(-20) = -20/2 = -10 Normalmente, la función inversa defse denota porf^1, pero por comodidad, ...

Asíntotas de funciones Informalmente, decimos que la función f tiene una asíntota en la recta r del plano real si la gráfica de f se acerca indefinidamente a la recta r. Ejemplo: La función f(x) = 1/x tiene asíntotas en las rectas y = 0 y x = 0: Las asíntotas pueden ser horizontales, verticales u oblicuas. La recta horizontal y = a es una asíntota horizontal de f si el límite de f(x) cuando x tiende a +infinito ó a -infinito es a. Ejemplo 1: La función exponencial f(x) = e^x tiene una ...

Exercicis Resolts de Matemàtiques Índex: Nombres: Mínim comú múltiple Màxim comú divisor Fraccions: Introducció a les fraccions Suma i resta de fraccions Multiplicació i divisió de fraccions Fracció generatriu de nombres decimals Fracció mixta o nombre mixt Potències: Calcular potències i simplificar expressions amb potències emprant les seves propietats Equacions de primer grau: Resoldre equacions Problems de plantejar equacio...

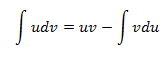Métodos de Integración Algunas primitivas se obtienen directamente a partir de la tabla de derivadas, este es el caso de las integrales directas o inmediatas, como por ejemplo: Sin embargo, lo habitual es que resolver una integral no sea una tarea fácil, razón por la que existen distintos métodos de integración. Los métodos básicos son: integración por partes integración por sustitución integración de funciones racionales Veamos un ejemplo de cada uno de ellos: 1. Int...