Ecuaciones de Segundo Grado

21/10/2021 Jose Llopis

Área de conocimiento

Contexto educativo

682 Visitas

Facebook Twitter

1. Introducción

Una ecuación de segundo grado puede escribirse en la forma

ecuación de segundo grado

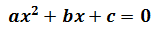
siendo siempre a distinto de 0 (si no, no es de segundo grado).

Decimos que la ecuación es completa cuando ninguno de los coeficientes, a,b y c es cero, es decir, cuando

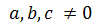
segundo grado incompleta coeficientes

Y decimos que la ecuación es incompleta cuando alguno de los coeficientes b ó c es cero.

Por tanto, una ecuación incompleta toma alguna de las siguientes formas

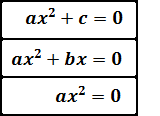
2. Ecuaciones Imcompletas

Si es de la forma

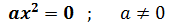
Tenemos la única solución (raíz doble) x = 0.

Si es de la forma

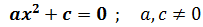
Despejando tenemos que

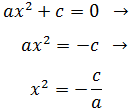
Haciendo la raíz cuadrada, obtenemos las dos raíces

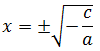
Pero es necesario que el radicando (interior de la raíz) sea positivo. Si no es así, no existen soluciones (reales).

Si es de la forma

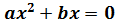
Factorizamos:

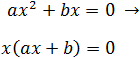
Como es un producto cuyo resultado es 0, alguno de los dos factores tiene que ser 0. Por tanto, tenemos las siguientes posibilidades (raíces):

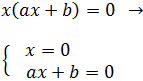
Es decir, una solución es x = 0 y la otra solución es x = -b/a.

Enlace: Resolución de Ecuaciones de Segundo Grado Incompletas

3. Ecuaciones Completas

Si es de la forma

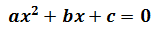
siendo a, b y c distintos de 0, entonces tenemos que aplicar la fórmula

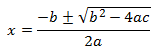
Al radicando de la fórmula

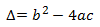
se le llama discriminante de la ecuación y su signo nos informa del tipo y número de soluciones:

a) Si Δ es 0, la ecuación tiene una única solución (de multiplicidad 2)
b) Si Δ es menor que 0, no existen soluciones (reales)
c) Si Δ es mayor que 0, existen dos soluciones (reales) distintas (de multiplicidad 1).
Enlaces:

Ecuaciones Resueltas:

Otros: