Área de un Triángulo
Área de un Triángulo
Principalmente, hay dos formas de calcular el área de un triángulo: la mitad de la base por altura y la fórmula de Herón.
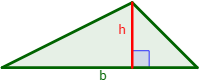
El área de un triángulo de altura h y base b es la mitad del producto de la altura por la la base:
área = b·h/2
Ejemplo: el triángulo equilátero (todos los lados miden lo mismo) de lado 3cm (y, por tanto, altura 2,6cm)

tiene área
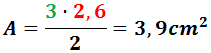
Una demostración intuitiva de esta fórmula consiste en cortar el triángulo para formar un cuadrado: áreas de triángulos (justificación de la fórmula)
.
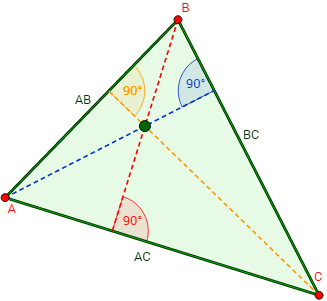
La altura del triángulo es el segmento que une un vértice con el lado opuesto (base) formando un ángulo recto (90 grados). Como hay 3 vértices, hay tres alturas (y tres bases).
Fórmula de Herón
La fórmula de Herón proporciona el área de un triángulo a partir de su semiperímetro s.
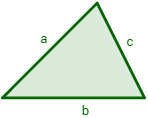
El área del triángulo de lados a, b y c es
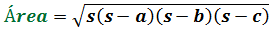
donde s es el semiperímetro de triángulo:
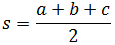
Ejemplo: el semiperímetro de un triángulo equilátero de lado 3cm es s = 9/2. Su área es la raíz cuadrada de 243/16 (aproximadamente, 3,9 centímetros cuadrados).
Enlaces:


Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.


