PROCOMÚN
Mostrando resultados 41 a 60 de un total de 255
-
Estudi de Funcions Algebraiques.pdf
 En aquest recurs l'alumnat de 4rt d'ESO de la matèria de matemàtiques B haurà d'estudiar les funcions algebraiques i les seues característiques utilitzant com a recurs didàctic adicional l'aplicatiu GeoGebra.Área de conocimientoContexto educativoTipo de recurso
En aquest recurs l'alumnat de 4rt d'ESO de la matèria de matemàtiques B haurà d'estudiar les funcions algebraiques i les seues característiques utilitzant com a recurs didàctic adicional l'aplicatiu GeoGebra.Área de conocimientoContexto educativoTipo de recurso -
funciones_geogebra_coef.pdf
 Funciones y GeoGebra: coeficientes con deslizador en la función lineal y cuadráticaÁrea de conocimientoContexto educativoTipo de recurso
Funciones y GeoGebra: coeficientes con deslizador en la función lineal y cuadráticaÁrea de conocimientoContexto educativoTipo de recurso -
Descubriendo los sistemas de ecuaciones.pdf
 • Tras una breve investigación sobre el origen de los sistemas de ecuaciones, el alumnado trabajará con Geogebra para evidenciar cómo cada una de las ecuaciones representa una recta y qué información puede obtenerse de cara a la resolución del sistema. • Una vez conocido el Geogebra, tratarán de hacer algo similar con el programa Excel, tras una explicación del docente. • Asimismo, descubrirán aplicaciones de los sistemas de ecuaciones en otras materias y en la vida real.Área de conocimientoContexto educativoTipo de recurso
• Tras una breve investigación sobre el origen de los sistemas de ecuaciones, el alumnado trabajará con Geogebra para evidenciar cómo cada una de las ecuaciones representa una recta y qué información puede obtenerse de cara a la resolución del sistema. • Una vez conocido el Geogebra, tratarán de hacer algo similar con el programa Excel, tras una explicación del docente. • Asimismo, descubrirán aplicaciones de los sistemas de ecuaciones en otras materias y en la vida real.Área de conocimientoContexto educativoTipo de recurso -
Evolución del uso de las redes sociales: Situación de Aprendizaje para 4º ESO - Matemáticas B
 Esta situación de aprendizaje está diseñada para alumnado de 4º de ESO, dentro del área de Matemáticas B. El alumnado investigará la evolución del uso de las redes sociales (TikTok, Instagram y X/Twitter) entre 2019 y 2024, buscará datos reales, elaborará gráficos estadísticos utilizando GeoGebra y reflexionará sobre el impacto social de estas plataformas. Incluye actividades de inclusión, ampliación para alumnado avanzado y rúbricas de evaluación y coevaluación. Fomenta la competencia matem...Área de conocimientoContexto educativoTipo de recurso
Esta situación de aprendizaje está diseñada para alumnado de 4º de ESO, dentro del área de Matemáticas B. El alumnado investigará la evolución del uso de las redes sociales (TikTok, Instagram y X/Twitter) entre 2019 y 2024, buscará datos reales, elaborará gráficos estadísticos utilizando GeoGebra y reflexionará sobre el impacto social de estas plataformas. Incluye actividades de inclusión, ampliación para alumnado avanzado y rúbricas de evaluación y coevaluación. Fomenta la competencia matem...Área de conocimientoContexto educativoTipo de recurso -
Evolución del uso de las redes sociales: Situación de Aprendizaje para 4º ESO - Matemáticas B
 Esta situación de aprendizaje está diseñada para alumnado de 4º de ESO, dentro del área de Matemáticas B. El alumnado investigará la evolución del uso de las redes sociales (TikTok, Instagram y X/Twitter) entre 2019 y 2024, buscará datos reales, elaborará gráficos estadísticos utilizando GeoGebra y reflexionará sobre el impacto social de estas plataformas. Incluye actividades de inclusión, ampliación para alumnado avanzado y rúbricas de evaluación y coevaluación. Fomenta la competencia matem...Área de conocimientoContexto educativoTipo de recurso
Esta situación de aprendizaje está diseñada para alumnado de 4º de ESO, dentro del área de Matemáticas B. El alumnado investigará la evolución del uso de las redes sociales (TikTok, Instagram y X/Twitter) entre 2019 y 2024, buscará datos reales, elaborará gráficos estadísticos utilizando GeoGebra y reflexionará sobre el impacto social de estas plataformas. Incluye actividades de inclusión, ampliación para alumnado avanzado y rúbricas de evaluación y coevaluación. Fomenta la competencia matem...Área de conocimientoContexto educativoTipo de recurso -
Evolución del uso de las redes sociales: Situación de Aprendizaje para 4º ESO - Matemáticas B
 Esta situación de aprendizaje está diseñada para alumnado de 4º de ESO, dentro del área de Matemáticas B. El alumnado investigará la evolución del uso de las redes sociales (TikTok, Instagram y X/Twitter) entre 2019 y 2024, buscará datos reales, elaborará gráficos estadísticos utilizando GeoGebra y reflexionará sobre el impacto social de estas plataformas. Incluye actividades de inclusión, ampliación para alumnado avanzado y rúbricas de evaluación y coevaluación. Fomenta la competencia matem...Área de conocimientoContexto educativoTipo de recurso
Esta situación de aprendizaje está diseñada para alumnado de 4º de ESO, dentro del área de Matemáticas B. El alumnado investigará la evolución del uso de las redes sociales (TikTok, Instagram y X/Twitter) entre 2019 y 2024, buscará datos reales, elaborará gráficos estadísticos utilizando GeoGebra y reflexionará sobre el impacto social de estas plataformas. Incluye actividades de inclusión, ampliación para alumnado avanzado y rúbricas de evaluación y coevaluación. Fomenta la competencia matem...Área de conocimientoContexto educativoTipo de recurso -
Ayuda para la documentación de la resolución ejercicios EVAU con Geogebra.pdf
 Ejemplo - Guía de cómo realizar la comprobación de los datos calculados al realizar los ejercicios propuestos de EVAU de Comunidad Valenciana. Este documento es un ejemplo de la actividad que se debe realizar. Este ejemplo se realizará en clase y se analizarán los distintos pasos que se ejecuten para su posterior documentación. Una vez calibradas las posibilidades que ofrece Geogebra, se elegirán de entre una lista de ejercicios reales de EVAU, dos ejercicios para realizar y documentar. E...Área de conocimientoContexto educativoTipo de recurso
Ejemplo - Guía de cómo realizar la comprobación de los datos calculados al realizar los ejercicios propuestos de EVAU de Comunidad Valenciana. Este documento es un ejemplo de la actividad que se debe realizar. Este ejemplo se realizará en clase y se analizarán los distintos pasos que se ejecuten para su posterior documentación. Una vez calibradas las posibilidades que ofrece Geogebra, se elegirán de entre una lista de ejercicios reales de EVAU, dos ejercicios para realizar y documentar. E...Área de conocimientoContexto educativoTipo de recurso -
SIESTEMES D'EQUACIONS LINEALS AMB GEOGEBRA
 En aquesta activitat amb el recurs GeoGebra pretenem que l'alumnat aprenga a reconèixer de manera interactiva i visual els tipus de solucions que es poden donar segons les posicions relatives de les equacions.Área de conocimientoContexto educativoTipo de recurso
En aquesta activitat amb el recurs GeoGebra pretenem que l'alumnat aprenga a reconèixer de manera interactiva i visual els tipus de solucions que es poden donar segons les posicions relatives de les equacions.Área de conocimientoContexto educativoTipo de recurso -
Estadística bidimensional amb GeoGebra
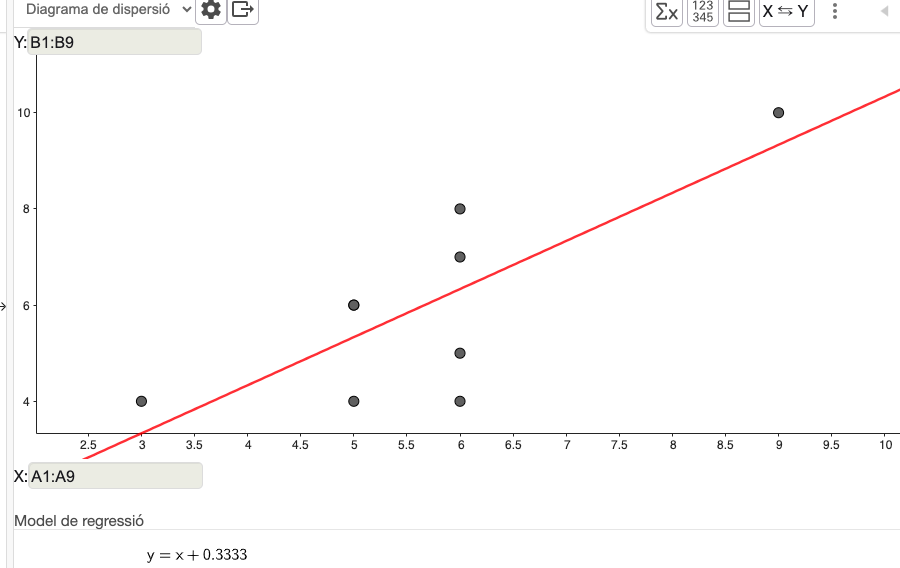 En aquesta tasca els alumnes treballen l'estadistica bidimensional amb el GeoGebra: aprenen a representar núvols de punts, trobar els estadístics adients, els diferents models i fer prediccions.Área de conocimientoContexto educativoTipo de recurso
En aquesta tasca els alumnes treballen l'estadistica bidimensional amb el GeoGebra: aprenen a representar núvols de punts, trobar els estadístics adients, els diferents models i fer prediccions.Área de conocimientoContexto educativoTipo de recurso -
Sistemes d'equacions.pdf
 Activitat i xicotet tutorial per a representar sistemes d'equacions amb l'aplicació web de Geogebra. Dirigit a alumnat de 4t ESO. Assignatura de matemàtiques. Dissenyada per a complementar la Situació d'Aprenentatge dedicada als sistemes d'equacions.Área de conocimientoContexto educativoTipo de recurso
Activitat i xicotet tutorial per a representar sistemes d'equacions amb l'aplicació web de Geogebra. Dirigit a alumnat de 4t ESO. Assignatura de matemàtiques. Dissenyada per a complementar la Situació d'Aprenentatge dedicada als sistemes d'equacions.Área de conocimientoContexto educativoTipo de recurso -
Representar Ecuaciones Lineales y Afines
 El alumnado realizará una actividad con Aules para demostrar que es capaz de realizar una representación de funciones con GeoGebra, guardar la información y adjuntarla en Aules para ser evaluada por el profesorado. Enlace: https://aules.edu.gva.es/eso46/course/view.php?id=342898Área de conocimientoContexto educativo
El alumnado realizará una actividad con Aules para demostrar que es capaz de realizar una representación de funciones con GeoGebra, guardar la información y adjuntarla en Aules para ser evaluada por el profesorado. Enlace: https://aules.edu.gva.es/eso46/course/view.php?id=342898Área de conocimientoContexto educativo -
Descobrim GeoGebra.pdf
 En aquesta activitat, l’alumnat tindrà un primer contacte amb GeoGebra Web, una eina tecnològica que permet visualitzar i experimentar amb conceptes matemàtics. A partir d’una presentació Power Point guiada, que es projectarà a l’aula, l’alumnat anirà seguint els passos a un ordinador portàtil facilitat pel centre. Durant l’activitat, aprendran a utilitzar les funcions bàsiques del programa i realitzaran construccions geomètriques. Es tracta d’una proposta pràctica, on cada alumne construeix ...Área de conocimientoContexto educativoTipo de recurso
En aquesta activitat, l’alumnat tindrà un primer contacte amb GeoGebra Web, una eina tecnològica que permet visualitzar i experimentar amb conceptes matemàtics. A partir d’una presentació Power Point guiada, que es projectarà a l’aula, l’alumnat anirà seguint els passos a un ordinador portàtil facilitat pel centre. Durant l’activitat, aprendran a utilitzar les funcions bàsiques del programa i realitzaran construccions geomètriques. Es tracta d’una proposta pràctica, on cada alumne construeix ...Área de conocimientoContexto educativoTipo de recurso -
Demostració del Teorema de Pitàgores
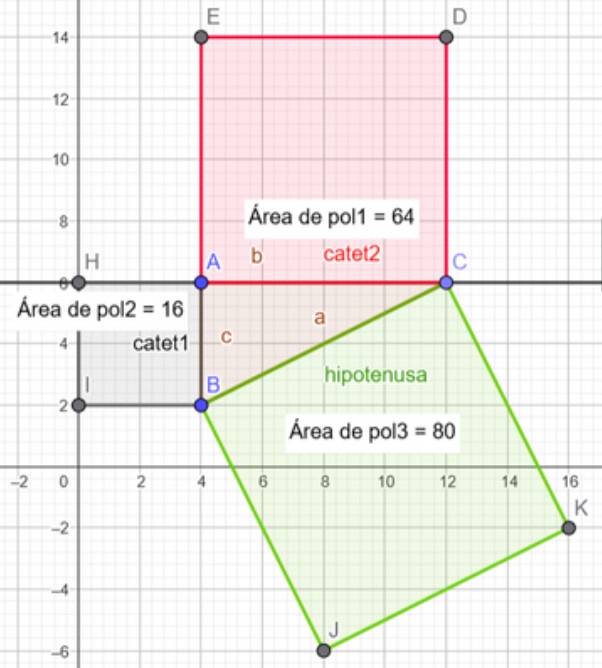 En esta actividad el alumnado utilizará Geogebra para construir un triángulo rectángulo y unos cuadrados en cada lado. De esta forma, observaran que se cumple el teorema de Pitágoras y lo que ocurre cuando cambian los vértices del triángulo.Área de conocimientoContexto educativoTipo de recurso
En esta actividad el alumnado utilizará Geogebra para construir un triángulo rectángulo y unos cuadrados en cada lado. De esta forma, observaran que se cumple el teorema de Pitágoras y lo que ocurre cuando cambian los vértices del triángulo.Área de conocimientoContexto educativoTipo de recurso -
PRÀTICA GEOGEBRA LIDIA PÉREZ SÁNCHEZ.pdf
 Práctica de GeoGebra para representar funcionesÁrea de conocimientoContexto educativoTipo de recurso
Práctica de GeoGebra para representar funcionesÁrea de conocimientoContexto educativoTipo de recurso -
Guia GeoGebra Funció Segon Grau
 Guia per a aprendre a crear i representar una funció de segon grau en GeoGebra. L'alumnat crearà una aplicació amb GeoGebra que represente una funció del tipus f(x)=ax2+bx+c. Modificaran els valors de a, b i c amb deslliçadors per observar canvis en la gràfica, identificant les arrels i altres característiques de la paràbola.Área de conocimientoContexto educativoTipo de recurso
Guia per a aprendre a crear i representar una funció de segon grau en GeoGebra. L'alumnat crearà una aplicació amb GeoGebra que represente una funció del tipus f(x)=ax2+bx+c. Modificaran els valors de a, b i c amb deslliçadors per observar canvis en la gràfica, identificant les arrels i altres característiques de la paràbola.Área de conocimientoContexto educativoTipo de recurso -
Comparativa de métodos de resolución de Sistemas Ecuaciones
 Enunciado de la tarea para realizar una comparativa entre los métodos de resolución de sistemas de ecuaciones lineales con 2 incógnitas utilizando las TICsÁrea de conocimientoContexto educativoTipo de recurso
Enunciado de la tarea para realizar una comparativa entre los métodos de resolución de sistemas de ecuaciones lineales con 2 incógnitas utilizando las TICsÁrea de conocimientoContexto educativoTipo de recurso -
Resolviendo sistemas con GeoGebra.zip
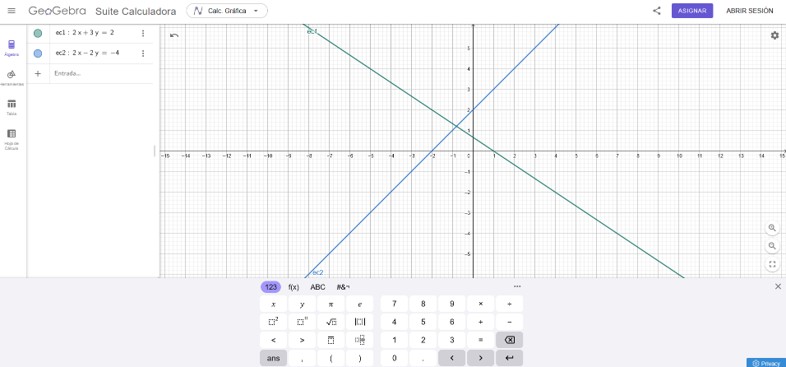 El software GeoGebra es una potente aplicación de geometría dinámica, además de calculadora gráfica. Con él podemos representar funciones de cualquier tipo, representaciones a nivel geométrica e incluso resolver ecuaciones de forma algebraica y analítica. Entre las múltiples opciones que ofrece, vamos a explorar las funciones gráficas, concretamente, la resolución de sistemas de ecuaciones de forma analítica y gráfica.Área de conocimientoContexto educativoTipo de recurso
El software GeoGebra es una potente aplicación de geometría dinámica, además de calculadora gráfica. Con él podemos representar funciones de cualquier tipo, representaciones a nivel geométrica e incluso resolver ecuaciones de forma algebraica y analítica. Entre las múltiples opciones que ofrece, vamos a explorar las funciones gráficas, concretamente, la resolución de sistemas de ecuaciones de forma analítica y gráfica.Área de conocimientoContexto educativoTipo de recurso -
Parábola del cumpleaños.pdf
 En este recurso se trabaja la gráfica de una función polinómica de segundo gradoÁrea de conocimientoContexto educativoTipo de recurso
En este recurso se trabaja la gráfica de una función polinómica de segundo gradoÁrea de conocimientoContexto educativoTipo de recurso -
InfografíaPIT.pdf
 Esquema d'introducció-presentació a situació d'aprenentatge indicant tots els passos que seguirà l'alumnat per a treballar la figura i continguts relacionats amb Pitàgores.Área de conocimientoContexto educativoTipo de recurso
Esquema d'introducció-presentació a situació d'aprenentatge indicant tots els passos que seguirà l'alumnat per a treballar la figura i continguts relacionats amb Pitàgores.Área de conocimientoContexto educativoTipo de recurso -
La función lineal
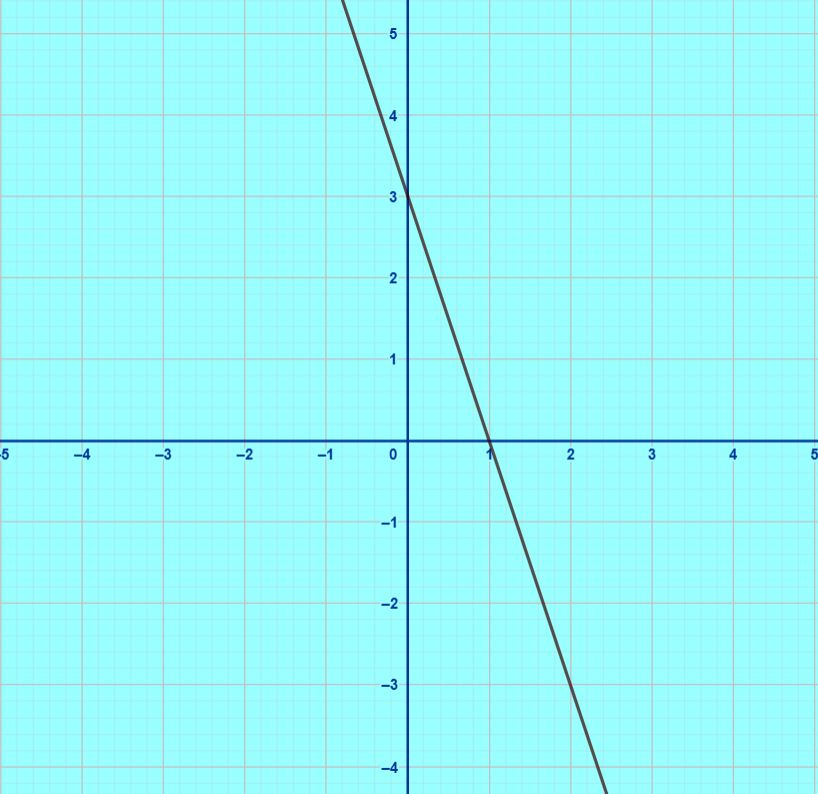 Breve explicación de la ecuación de la función lineal para identificar pendiente y ordenada en el origen, acompañada de una actividad interactiva de Geogebra para observar los cambios en la recta al modificar ambos parámetros. Matemáticas 3ºESO.Área de conocimientoContexto educativoTipo de recurso
Breve explicación de la ecuación de la función lineal para identificar pendiente y ordenada en el origen, acompañada de una actividad interactiva de Geogebra para observar los cambios en la recta al modificar ambos parámetros. Matemáticas 3ºESO.Área de conocimientoContexto educativoTipo de recurso


