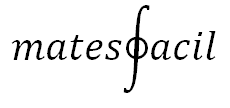
Equacions exponencials i logarítmiques 1. Equacions exponencials Una equació exponencial és aquella en la que apareixen exponencials, és a dir, potències que tenen la incògnita, x, en els exponents. En aquesta pàgina resoldrem equacions exponencials sense emprar logaritmes. El mètode de resolució consisteix en aconseguir una igualtat entre dues exponencials amb la mateixa base per poder igualar els seus exponents. Aplicarem les propietats de les potències. Exemple 1: Si escrivim 27 com...

Análisis de un #REA_INTEF Blender: 3D en la Educación Estructura y organización -objetivos -contenidos -secuencia de actividades -autoevaluación indicadores competenciales criterios de evaluación a definir en su reutilización en el aula Aplicación en el aula Diseño de mobiliario (3d) -Temas de construcción y mapeado. -vídeos explicativos (proyectar aula + en casa) -ejercicios c...

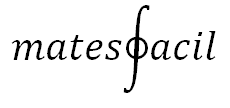
Ecuaciones Exponenciales Una ecuación exponencial es aquella en la que aparecen exponenciales, es decir, potencias cuyos exponentes son expresiones en las que aparece la incógnita, x. En esta sección, resolveremos ecuaciones exponenciales sin usar logaritmos. El método de resolución consiste en conseguir una igualdad de exponenciales con la misma base para poder igualar los exponentes. Para ello, utilizaremos las propiedades de las potencias. Ejemplo 1: Escribimos 16 como una potencia ...

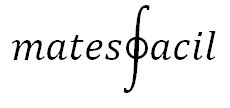
Logarithmic Equations and Systems A logarithmic equation is an equation that has an unknown factor in the argument of a logarithm. In reality, the resolution is reduced to the resolution of equations of the same type as the expressions in the arguments (quadratic equations, cubic equations, irrational equations...). Before starting the exercises, let's remember the logarithmic properties: Logarithm of a product: Logarithm of a quotient: Logarithm of a power: Change of base: Use...

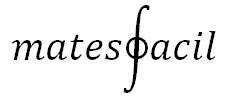
Asíntotas de funciones Informalmente, decimos que la función f tiene una asíntota en la recta r del plano real si la gráfica de f se acerca indefinidamente a la recta r. Ejemplo: La función f(x) = 1/x tiene asíntotas en las rectas y = 0 y x = 0: Las asíntotas pueden ser horizontales, verticales u oblicuas. La recta horizontal y = a es una asíntota horizontal de f si el límite de f(x) cuando x tiende a +infinito ó a -infinito es a. Ejemplo 1: La función exponencial f(x) = e^x tiene una ...

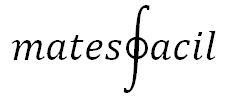
Matrices y Sistemas de Ecuaciones Lineales (SEL) 1. Definición de SEL y su solución Un sistema de m ecuaciones lineales con n incógnitas (SEL) y coeficientes en un cuerpo K (como los reales o los complejos) es A los elementos ai,j se les denomina coeficientes del SEL y a los b_i términos independientes. Un ejemplo de un SEL de dos ecuaciones y dos incógnitas es Dimensión del SEL: dimensión cuadrada: si m = n (tiene el mismo número de ecuaciones que de incógnitas). dimensión...

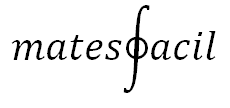
En este artículo vamos a obtener una fórmula para calcular la derivada de una función elevada a otra función, por ejemplo: 1. La fórmula Sea la función y(x) la que queremos derivar. Supongamos que es de la forma: Es decir, la función y(x) es la función f(x) elevada a la función g(x). Para facilitar la notación, escribimos y, f y g para referirnos a las funciones y(x), f(x) y g(x), respectivamente. Las derivadas de estas funciones las escribiremos como y', f' y g'. Por tanto, la funci...

La herramienta de Google académico, más conocido por muchos en nombre en inglés "Google Scholar", es un buscador de Google experto en artículos desde un enfoque académico, y soportado por una base de datos libre desde Internet que guarda un extenso conjunto de trabajos de investigación científica de diferentes disciplinas y en diferentes formatos de publicación. Un ejemplo: Si buscamos "arquitectura" nos lanza alrededor de 900.000 Mil links entre libros en su mayoría en formato PDF, artículo ...

APP que da las pautas a seguir para evitar una parada respiratoria

Mi Ple

Comparto la entrada en mi blog "Guión narrativo, storyboard y rúbrica #EduNarraMooc" http://seveizquierdo.blogspot.com.es/2015/10/guion-narrativo-storyboard-y-rubrica.html

Comparto la entrada en mi blogCrea tu Narracurriculum Digital #EduNarraMooc http://seveizquierdo.blogspot.com.es/2015/10/crea-tu-narracurriculum-digital.html

Comparto la entrada en mi blogCrea tu Narracurriculum Digital #EduNarraMooc http://seveizquierdo.blogspot.com.es/2015/10/crea-tu-narracurriculum-digital.html

Os presento el proyecto colaborativo Tertulias con sabor a chocolate “una iniciativa centrada en la comunicación oral, en el diálogo, en la palabra sentida, imaginada, pensada, en la palabra que encuentra oportunidad y espacio para ser hablada y escuchada, en la palabra que, adentrándose en el universo del otro, va tejiendo respuesta...” en la que “...resuena la tradición de las comunidades de investigación fIlosófica, de las comunidades de aprendizaje, de las comunidades dialógicas” (1) Es ...

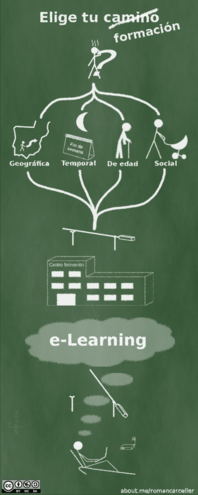
Os dejo esta infografía que explica las barreras que el e-Learning ha conseguido abrir para facilitar la formación a las personas con alguna dificultad para acceder a la educación tradicional. Fuente de información: e-Learning: antecedentes. Carlos Marcelo García - Formación en Red del INTEF Letras efecto pizarra en GIMP

La Web 2.0 ha establecido nuevas formas de comunicación, de aprendizaje, etc., por ello, la presencia en la red, es decir, la presencia digital ha fomentado la creación de los Entornos Personales de Aprendizaje, también conocidos como PLE, acrónimo inglés de Personal Learning Enviroment, por ello, os dejo el mio. PLE Mónica MoyafromMónica Moya López Sobre los PLE aconsejo el siguiente taller de Linda Castañeda, que ayuda a entender la idea de PLE: https://sites.google.com...

Debemos considerar que el mundo profesional de la fotografía escapa a muchos usuarios que no queremos llegar a ese punto tan álgido, pero a la vez, como amateurs queremos comprender y poder realizar fotografías que por lo menos reflejen la realidad, un sentimiento. Me he preguntadocómo me gustaría aprender a fotografiar paisajes, entornos naturales o urbanos sin perder esa esencia, en este sentido, la opción más viable es mostraros una serie deinfografías sobre fotografía.Desde los component...

A continuación, se presenta una infografía sobre las diferentes herramientas y recursos que empleo en mi día a día para formarme y desarrollar mi labor profesional. Aunque es una infografía de carácter personal, puede servir, a cualquiera, para saber de la existencia de estas herramientas y recursos de gestión, síntesis y análisis de contenidos: https://virjari.wordpress.com/2015/03/08/comienzo-del-curso-de-tutores-para-formacion-en-red/