Polígonos I Un polígono es una figura geométrica formada por segmentos rectos (llamados lados) unidos de forma que encierran un área en el plano. Ejemplos: polígonos de cinco lados (pentágonos) Estos polígonos se denominan pentágonos puesto que tienen cinco lados. Un polígono es regular cuando todos sus lados tienen la misma longitud y los ángulos (interiores) que forman los lados son iguales. Si no es así, el polígono es irregular. Ejemplo: polígonos regulares El nombre de un políg...

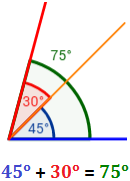
Un ángulo es la región del plano comprendida entre dos semirrectas con origen común:  Si dividimos una circunferencia en 360 partes iguales, un grado sexagesimal es una de estas partes. Un grado se expresa como 1º:  Para medir un ángulo, éste se coloca sobre el diagrama anterior: Al colocar el ángulo rojo sobre la circunferencia observamos que éste mide 30º (30 grados sexagesimales). Minutos y segundos sexagesimales Si dividimos un grado sexagesimal en 60 partes iguales, cada una...

Equacions de segon grau completes i incompletes Una equació de segon grau és una equació polinòmica de grau 2, és a dir, el major grau dels monomis és 2, o siga, x al quadrat. Com que l'equació és de grau 2, tindrà, com a molt, dues arrels (solucions) distintes. Tota equació de segon grau es pot escriure en la forma Si ningun dels coeficients, a,b i c és zero, és a dir, direm que l'equació és completa. Si no és així (si b ó c és 0), direm que és incompleta. 1. Equació completa Les...

Si conocemos dos lados de un triángulo rectángulo, podemos calcular el otro lado aplicando el teorema de Pitágoras. Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno. El coseno de un ángulo α se define como el cociente del lado contiguo al ángulo α y la hipotenusa. De forma análoga, el seno de α se define como el cociente del lado opuesto al ángulo α y la hipotenusa. Nota: si...

Pythagoren Theorem Pythagoras' Theorem: Given a right triangle with sides a and b and a hypotenuse h (the side opposite the right angle). Then, Remember that... triangle is a right-angled triangle because it has a right angle, an angle of 90º or π / 2 radians The hypotenuse is the opposite side as the right angle. Note: h is always bigger than the other sides, as shows h > a and h > b. The Pythagoras theorem is one of the most known results in mathematics and also one...

Mínim comú múltiple i màxim comú divisor 1. Descomposició de nombres Per a calcular el mínim comú múltiple o el màxim comú divisor de dos o més nombres cal descompondre aquests com un producte de potències de nombres primers. Exemple: Per descompondre un nombre dividim el nombre successivament entre nombres primers fins obtenir un 1. Més concretament: Dividim successivament per nombres primers (de manera que la divisió sigui exacta). La descomposició és el producte de les potències d...

Teorema de Pitàgores Teorema i exemples d'aplicació. 1. Teorema de Pitàgores Donat un triangle rectangle amb catets a i b i hipotenusa h (el costat oposat a l'angle recte). Aleshores, Recordem que: el triangle és rectangle perquè té un angle recte, és a dir, un angle de 90 graus ó π / 2 radiants. la hipotenusa és el costat oposat a l'angle recte Problemes d'aplicació Problema 1 Calcular la hipotenusa del triangle rectangle de costats 3cm i 4cm. Solució: Els costats só...

Proporcionalidad directa Dos magnitudes a y b son directamente proporcionales cuando existe una constante k tal que a/b = k La constante k se denomina constante de proporcionalidad o razón. Se dice que a y b mantienen una relación de proporcionalidad directa. En la proporcionalidad directa, cuando una de las magnitudes cambia, la otra también debe hacerlo de modo que su razón se mantenga constante. Ejemplo: En un movimiento con velocidad constante v, la distancia recorrida viene dada p...

Mi Ple