PROCOMÚN
Mostrando os resultados do 1 ao 5 dun total de 5
-
funcions lineal i afí amb geogebra complet_1.pdf
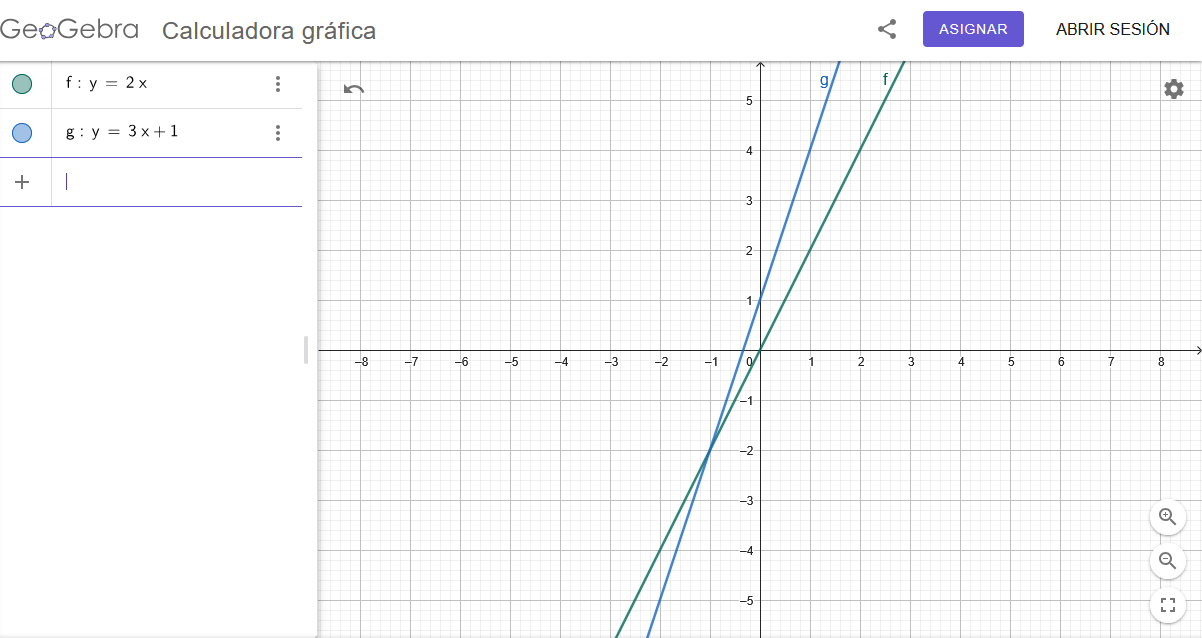 Explicació i exercicis de les funcions lineal i afins.Área de coñecementoContexto educativoTipo de recurso
Explicació i exercicis de les funcions lineal i afins.Área de coñecementoContexto educativoTipo de recurso -
Matemáticas en la feria
 Esta SA trabaja las funciones lineales, afines, cuadráicas e inversas para alumnado de 2º ESO, a través de pequeñas tareas guiadas de deducción e investigación, búsqueda de aplicación a situaciones cotidianas y la elaboración de un producto final relacionado con el diseño de una atracción de feria a partir de las funciones estudiadas.Área de coñecementoContexto educativoTipo de recurso
Esta SA trabaja las funciones lineales, afines, cuadráicas e inversas para alumnado de 2º ESO, a través de pequeñas tareas guiadas de deducción e investigación, búsqueda de aplicación a situaciones cotidianas y la elaboración de un producto final relacionado con el diseño de una atracción de feria a partir de las funciones estudiadas.Área de coñecementoContexto educativoTipo de recurso -
Memoria final. La Función Lineal
Esta actividad pretende ser una herramienta para profesorado y alumnos en el proceso enseñanza-aprendizaje de la función de proporcionalidad directa e interpretar la pendiente de la misma. Para ello se usará un programa (proyecto Scratch) como a continuación se describe, el cual podría formar parte de un ODE ( Objeto Digital Educativo) realizado con Exelearning u otra herramienta y posteriormente publicado.Área de coñecemento -
Funciones lineales (rectas)
 Definimos función lineal, calculamos los puntos de corte con los ejes de coordenadas y explicamos cómo calcular la recta que pasa por dos puntos. Con ejemplos.Enlaces con problemas de funciones:Dominio y recorrido (1)Dominio y recorrido (2)Funciones linealesFunciones cuadráticasRectas y parábolasFunciones polinómicasFunciones definidas a trozos (1)Funciones definidas a trozos (2)Problemas de funciones (1)Problemas de funciones (2)Funciones continuas (1)Funciones continuas (2)Función inversa (...Área de coñecementoContexto educativoTipo de recurso
Definimos función lineal, calculamos los puntos de corte con los ejes de coordenadas y explicamos cómo calcular la recta que pasa por dos puntos. Con ejemplos.Enlaces con problemas de funciones:Dominio y recorrido (1)Dominio y recorrido (2)Funciones linealesFunciones cuadráticasRectas y parábolasFunciones polinómicasFunciones definidas a trozos (1)Funciones definidas a trozos (2)Problemas de funciones (1)Problemas de funciones (2)Funciones continuas (1)Funciones continuas (2)Función inversa (...Área de coñecementoContexto educativoTipo de recurso -
Función lineal
 Este objeto educativo forma parte del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra, esta actividad propone encontrar la expresión algebraica de cualquier función cuya gráfica corresponda a una recta que pase por el origen de coordenadas. Se obtiene la ecuación explícita de la recta utilizando lugares geométricos. Se estudia también la pendiente de la recta.Área de coñecementoContexto educativoTipo de recursoColecciones
Este objeto educativo forma parte del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra, esta actividad propone encontrar la expresión algebraica de cualquier función cuya gráfica corresponda a una recta que pase por el origen de coordenadas. Se obtiene la ecuación explícita de la recta utilizando lugares geométricos. Se estudia también la pendiente de la recta.Área de coñecementoContexto educativoTipo de recursoColecciones


