En este artículo vamos a obtener una fórmula para calcular la derivada de una función elevada a otra función, por ejemplo: 1. La fórmula Sea la función y(x) la que queremos derivar. Supongamos que es de la forma: Es decir, la función y(x) es la función f(x) elevada a la función g(x). Para facilitar la notación, escribimos y, f y g para referirnos a las funciones y(x), f(x) y g(x), respectivamente. Las derivadas de estas funciones las escribiremos como y', f' y g'. Por tanto, la funci...

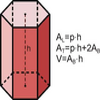Ilustración de la figura geométrica de un prisma y de las fórmulas para hallar sus áreas lateral y total, y su volumen

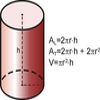Ilustración de la figura geométrica de un cilindro y de las fórmulas para hallar sus áreas lateral y total, y su volumen

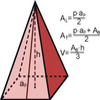Ilustración de la figura geométrica de una pirámide y de las fórmulas para hallar sus áreas lateral y total, y su volumen

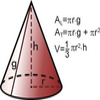Ilustración de la figura geométrica de un cono y de las fórmulas para hallar sus áreas lateral y total, y su volumen

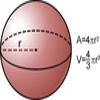Ilustración de la figura geométrica de una esfera y de la fórmula para hallar su área y su volumen

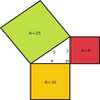Ilustración del Teorema de Pitágoras mediante las figuras geométricas de tres cuadrados con sus áreas, cada uno de ellos compartiendo uno de los lados con los de un triángulo rectángulo