Collage utilizando la aplicación "KD Collage", en donde cada foto deberá incluir un QR generado por la aplicación "Unitage" y lo entregará en formato pdf, adjuntado a la tarea propuesta en "Classroom". Cada QR hará referencia a una figura geométrica plana o espacial, simple o compuesta, expresando sus dimensiones, en la que se pretenda calcular el área de la figura plana o el volumen en el caso de figura espacial (cuerpo geométrico), evaluando las posibles soluciones que pueden darse relacion...

Os presento en el siguiente enlace el trabajo de centro con 12 lesson plans elaboradas por el equipo SymbalooEDU del colegio, 12 compañeros que hemos cursado “Aprendizaje personalizado en entornos digitales”. URL: Webmix-Colegio La Merced-Jesuitas-Burgos Centro educativo: La Merced y San Francisco Javier”. Jesuitas. Burgos. El boceto de centro se diseñó siguiendo un mismo hilo conductor en el centro: “El comercio”. De esta forma, los contenidos que se trabajan en los itinerarios giran en...

Movimiento Rectilíneo Uniforme El movimiento es rectilíneo uniforme cuando la trayectoria es una línea recta y la velocidad es constante (no existe aceleración). En este movimiento, la distancia recorrida, x, es proporcional al tiempo, t, y a la velocidad, v: x = v·t Por tanto, cuanto más tiempo dure el desplazamiento o cuanto mayor sea la velocidad, mayor es la distancia recorrida. 1. Datos iniciales Si el movimiento comienza en la posición x0 y en el tiempo t0, entonces la posición ...

Si conocemos dos lados de un triángulo rectángulo, podemos calcular el otro lado aplicando el teorema de Pitágoras. Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno. El coseno de un ángulo α se define como el cociente del lado contiguo al ángulo α y la hipotenusa. De forma análoga, el seno de α se define como el cociente del lado opuesto al ángulo α y la hipotenusa. Nota: si...

Hola, en el siguiente enlace pueden encontrar ejercicios interactivos de matemáticas. Son ejercicios con auto-corrección de álgebra, operaciones entre enteros, tablas de multiplicar.... Además, en la misma web Matesfacil.com, pueden encontrar apuntes y problemas resueltos de matemáticas para secundaria y bachillerato. Un saludo. Enlace: Ejercicios interactivos Otros: Problemas y Ecuaciones Ecuaciones Resueltas

Cálculo de Ráices Cuadradas Vamos a ver las partes de una raíz cuadrada y el algoritmo (método) para calcular la raíz cuadrada de un número. Partes de una raíz cuadrada: El radicando es el número cuya raíz queremos calcular. Es decir, si b es el radicando y aes la raíz de b, entonces a al cuadrado es b. El radicando se escribe bajo el signo radical. Por ejemplo, si el radicando es 4, entonces la raíz cuadrada es 2 ya que 2 al cuadrado es 4. Si la raíz cuadrada no es número exacto (o se...

Pythagoren Theorem Pythagoras' Theorem: Given a right triangle with sides a and b and a hypotenuse h (the side opposite the right angle). Then, Remember that... triangle is a right-angled triangle because it has a right angle, an angle of 90º or π / 2 radians The hypotenuse is the opposite side as the right angle. Note: h is always bigger than the other sides, as shows h > a and h > b. The Pythagoras theorem is one of the most known results in mathematics and also one...

Exercicis Resolts de Matemàtiques Índex: Nombres: Mínim comú múltiple Màxim comú divisor Fraccions: Introducció a les fraccions Suma i resta de fraccions Multiplicació i divisió de fraccions Fracció generatriu de nombres decimals Fracció mixta o nombre mixt Potències: Calcular potències i simplificar expressions amb potències emprant les seves propietats Equacions de primer grau: Resoldre equacions Problems de plantejar equacio...

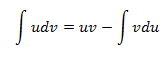Métodos de Integración Algunas primitivas se obtienen directamente a partir de la tabla de derivadas, este es el caso de las integrales directas o inmediatas, como por ejemplo: Sin embargo, lo habitual es que resolver una integral no sea una tarea fácil, razón por la que existen distintos métodos de integración. Los métodos básicos son: integración por partes integración por sustitución integración de funciones racionales Veamos un ejemplo de cada uno de ellos: 1. Int...

Fraccions Contingut:Introducció, Suma i resta de fraccions,Producte i divisió de fraccions,Fracció generatriu de nombres decimals,Fracció mixta (o nombre mixt) 1. Introducció Una fracció és una manera de representar la divisió de dos nombres. Es representa escrivint el dividend dalt d'una línia i el divisor baix d'aquesta. Exemple: fracció 3 partit 4 S'anomena numerador al nombre de dalt (en l'exemple, el 3) i denominador al nombre de baix (en l'exemple, el 4). La fracció de l'exempl...

Equacions de primer grau y sistemes En les equacions de primer grau la part literal dels monomis no tenen exponent major que 1 (per exemple, 3x pot aparèixer a una equació de primer grau però, x al quadrat no perquè és un monomi de segon grau). Precisament aquest fet ens assegura que, en cas d'existir solució, només n'hi ha una (excepte el cas especial en què n'hi ha infinites). Consells a l'hora de resoldre una equació 1. Si arribem a una igualtat impossible, no hi ha solució. Per exemple...

Clasificación de Triángulos 1. Concepto Un triángulo es un polígono de tres lados: Los vértices del triángulo son los puntos A, B y C. Los lados son los segmentos AB, BC y AC (llamados así para indicar los dos vértices que une cada uno de ellos). En todos los triángulos, los ángulos interiores que forman los lados suman siempre 180 grados: Ejemplo: La suma de los ángulos interiores es 50º+100º+30º = 180º Los ángulos exteriores son los que forman los lados con la prolongación del ...

Un porcentaje es una proporción tomando como referencia el número 100. Se expresa con un número seguido del signo %. Ejemplo 1: El 50% es la mitad ya que 50 es la mitad de 100. El 50% de 200 es 100. Ejemplo 2: El veinte por ciento (20%) es la quinta parte ya que 20 es la quinta parte de 100. El 20% de 500 es 100. Ejemplo 3: El 100% es el total ya que 100 es el total de 100. El 100% de 250 es 250. Cálculo de un porcentaje Los porcentajes son siempre relaciones de proporcio...

Mínim comú múltiple i màxim comú divisor 1. Descomposició de nombres Per a calcular el mínim comú múltiple o el màxim comú divisor de dos o més nombres cal descompondre aquests com un producte de potències de nombres primers. Exemple: Per descompondre un nombre dividim el nombre successivament entre nombres primers fins obtenir un 1. Més concretament: Dividim successivament per nombres primers (de manera que la divisió sigui exacta). La descomposició és el producte de les potències d...

Teorema de Pitàgores Teorema i exemples d'aplicació. 1. Teorema de Pitàgores Donat un triangle rectangle amb catets a i b i hipotenusa h (el costat oposat a l'angle recte). Aleshores, Recordem que: el triangle és rectangle perquè té un angle recte, és a dir, un angle de 90 graus ó π / 2 radiants. la hipotenusa és el costat oposat a l'angle recte Problemes d'aplicació Problema 1 Calcular la hipotenusa del triangle rectangle de costats 3cm i 4cm. Solució: Els costats só...

Os presento el proyecto colaborativo Tertulias con sabor a chocolate “una iniciativa centrada en la comunicación oral, en el diálogo, en la palabra sentida, imaginada, pensada, en la palabra que encuentra oportunidad y espacio para ser hablada y escuchada, en la palabra que, adentrándose en el universo del otro, va tejiendo respuesta...” en la que “...resuena la tradición de las comunidades de investigación fIlosófica, de las comunidades de aprendizaje, de las comunidades dialógicas” (1) Es ...

En el año 2000, Año Mundial de las Matemáticas, se instituyó la celebración del día 12 de mayo como Día Escolar de las Matemáticas por la Federación Española de Sociedades de Profesores de Matemáticas (FESPM). Esta fecha fue elegida en honor a Pedro Puig Adam, nacido el 12 de mayo de 1900 e internacionalmente reconocido en el campo de la enseñanza de las Matemáticas. Las diferentes Sociedades de Profes...

Wiki dedicada a la investigación sobre Gamificación aplicada a la educación, realizada por profesores y para profesores. El objetivo es elaborar un esquema práctico sobre los pasos necesarios para diseñar un sistema gamificado general que pueda ser personalizado según las necesidades de cada docente y grupo. La estructura general podrá ser completada con la sabiduría atesorada por los miembros de este grupo al aplicar la gamificaci&oacut...

La UOC oferta un MOOC dirigido a los docentes que deseen participar en el proyecto Hands-On ICT con la finalidad principal de crear una actividad aplicable a la realidad del aula utilizando herramientas TIC (learning design studio). La fecha de inicio era ayer, 27 de octubre, pero las inscripciones siguen abiertes. Los materiales están en inglés pero los foros se proponen en diferentes lenguas.