PROCOMÚN
Mostrando os resultados do 321 ao 340 dun total de 1707
-
EATINGBOOKS_ARANZAZUGARCIA.pdf
 El tema central es la comida desde varios puntos de vista: como ritual social, alimentación, su tratamiento en la literatura, los orígenes de la comida, el tratamiento que se da a los productos hasta que llegan a la mesa... Para los niveles de 3º y 4º de la ESO.Área de coñecementoContexto educativoTipo de recurso
El tema central es la comida desde varios puntos de vista: como ritual social, alimentación, su tratamiento en la literatura, los orígenes de la comida, el tratamiento que se da a los productos hasta que llegan a la mesa... Para los niveles de 3º y 4º de la ESO.Área de coñecementoContexto educativoTipo de recurso -
El universo y el álgebra
 UNIDAD DIDÁCTICA. EL UNIVERSO. ÁLGEBRA. 1º ESO. ÁMBITO.Área de coñecementoContexto educativoTipo de recurso
UNIDAD DIDÁCTICA. EL UNIVERSO. ÁLGEBRA. 1º ESO. ÁMBITO.Área de coñecementoContexto educativoTipo de recurso -
VECTORES
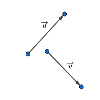 Tema de Vectores de 1º de Bachillerato de Matemáticas IÁrea de coñecementoContexto educativoTipo de recurso
Tema de Vectores de 1º de Bachillerato de Matemáticas IÁrea de coñecementoContexto educativoTipo de recurso -
Vectores
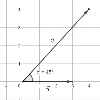 Tema de Vectores de 1º de Bachillerato de Matemáticas IÁrea de coñecementoContexto educativoTipo de recurso
Tema de Vectores de 1º de Bachillerato de Matemáticas IÁrea de coñecementoContexto educativoTipo de recurso -
¿Para qué sirven las matemáticas?
 ODE para darle sentido a algunos conocimientos básicos de la asignatura de matemáticas de 1º de ESO.Área de coñecementoContexto educativoTipo de recurso
ODE para darle sentido a algunos conocimientos básicos de la asignatura de matemáticas de 1º de ESO.Área de coñecementoContexto educativoTipo de recurso -
Álgebra: Expresiones Algebraicas
 Se maneja información que permite a los estudiantes comprender qué es una expresión algebraica y cómo convertir el lenguaje común al lenguaje algebraico, empleando a los valores desconocidos como literales.Área de coñecementoContexto educativoTipo de recurso
Se maneja información que permite a los estudiantes comprender qué es una expresión algebraica y cómo convertir el lenguaje común al lenguaje algebraico, empleando a los valores desconocidos como literales.Área de coñecementoContexto educativoTipo de recurso -
Sistemas de numeración
 En nuestro uso diario hacemos uso de distintos sistemas de numeración que tenemos interiorizados. En informática existen distintos sistemas de numeración que no son habituales en el uso cotidiano. ¡Vamos a aprender cuáles son!Área de coñecementoContexto educativoTipo de recurso
En nuestro uso diario hacemos uso de distintos sistemas de numeración que tenemos interiorizados. En informática existen distintos sistemas de numeración que no son habituales en el uso cotidiano. ¡Vamos a aprender cuáles son!Área de coñecementoContexto educativoTipo de recurso -
Las letras y los números se pueden llevar bien
 Simulación de una unidad de Matemáticas de 3º ESO. El propósito principal es ir avanzando materia paso a paso, recordando lo visto en anteriores cursos y añadiendo lo correspondiente al curso actual. Se empieza con una introducción para poco a poco ir adentrándonos en el mundo del álgebra. Primero con polinomios y finalmente, con su aplicación más conocida, las ecuaciones. Cuenta también con un número de tareas a realizar, enlaces de vídeos y material de apoyo, tanto para ampliación como para...Área de coñecementoContexto educativoTipo de recurso
Simulación de una unidad de Matemáticas de 3º ESO. El propósito principal es ir avanzando materia paso a paso, recordando lo visto en anteriores cursos y añadiendo lo correspondiente al curso actual. Se empieza con una introducción para poco a poco ir adentrándonos en el mundo del álgebra. Primero con polinomios y finalmente, con su aplicación más conocida, las ecuaciones. Cuenta también con un número de tareas a realizar, enlaces de vídeos y material de apoyo, tanto para ampliación como para...Área de coñecementoContexto educativoTipo de recurso -
Mobile Learning y RA-Aplicaciones en la Geometría Plana y Espacial
 Collage utilizando la aplicación "KD Collage", en donde cada foto deberá incluir un QR generado por la aplicación "Unitage" y lo entregará en formato pdf, adjuntado a la tarea propuesta en "Classroom". Cada QR hará referencia a una figura geométrica plana o espacial, simple o compuesta, expresando sus dimensiones, en la que se pretenda calcular el área de la figura plana o el volumen en el caso de figura espacial (cuerpo geométrico), evaluando las posibles soluciones que pueden darse relacion...Área de coñecementoContexto educativoTipo de recurso
Collage utilizando la aplicación "KD Collage", en donde cada foto deberá incluir un QR generado por la aplicación "Unitage" y lo entregará en formato pdf, adjuntado a la tarea propuesta en "Classroom". Cada QR hará referencia a una figura geométrica plana o espacial, simple o compuesta, expresando sus dimensiones, en la que se pretenda calcular el área de la figura plana o el volumen en el caso de figura espacial (cuerpo geométrico), evaluando las posibles soluciones que pueden darse relacion...Área de coñecementoContexto educativoTipo de recurso -
CÁLCULO DE DERIVADAS Y APLICACIONES EN 1º BACHILLERATO - ACTIVIDADES Y RECURSOS
 En esta Página Web de elaboración propia trataremos los contenidos que forman la unidad didáctica Cálculo de derivadas y aplicaciones, perteneciente al Bloque de Análisis del curso de 1º Bachillerato de Ciencias y Tecnología (Modalidad de Ciencias). Los contenidos que se tratarán, de forma general, son los siguientes: - Derivada de una función en un punto. - Interpretación geométrica de la derivada de una función en un punto. - Función derivada. - Cálculo de derivadas. - Álgebra de las deriva...Área de coñecementoContexto educativoTipo de recurso
En esta Página Web de elaboración propia trataremos los contenidos que forman la unidad didáctica Cálculo de derivadas y aplicaciones, perteneciente al Bloque de Análisis del curso de 1º Bachillerato de Ciencias y Tecnología (Modalidad de Ciencias). Los contenidos que se tratarán, de forma general, son los siguientes: - Derivada de una función en un punto. - Interpretación geométrica de la derivada de una función en un punto. - Función derivada. - Cálculo de derivadas. - Álgebra de las deriva...Área de coñecementoContexto educativoTipo de recurso -
1º ESO Matemáticas CIDEAD
 Recursos CIDEAD. Trsitemente no disponibles de forama editable ni a traves de su pagina oficialÁrea de coñecementoContexto educativoTipo de recurso
Recursos CIDEAD. Trsitemente no disponibles de forama editable ni a traves de su pagina oficialÁrea de coñecementoContexto educativoTipo de recurso -
4º ESO Matemáticas Aplicadas CIDEAD
 Recursos 4º ESO Matemáticas Aplicadas CIDEADÁrea de coñecementoContexto educativoTipo de recurso
Recursos 4º ESO Matemáticas Aplicadas CIDEADÁrea de coñecementoContexto educativoTipo de recurso -
Límites de una función y continuidad
Área de coñecementoContexto educativo -
Matrices (matemáticas)
 Matrices: concepto, suma, producto, transpuesta, determinante, adjunta e inversa. 1. Concepto de Matriz y operaciones básicas 1.1. Concepto Una matriz es un conjunto ordenado de números. Los números están ordenados por filas y por columnas. La dimensión de una matriz es m x n, siendo m el número de filas y n el número de columnas. Cuando m = n, se dice que la matriz es una matriz cuadrada de dimensión m. Ejemplo de una matriz: Esta matriz tiene 3 filas y 3 columnas. Por tanto, es una...Área de coñecementoContexto educativo
Matrices: concepto, suma, producto, transpuesta, determinante, adjunta e inversa. 1. Concepto de Matriz y operaciones básicas 1.1. Concepto Una matriz es un conjunto ordenado de números. Los números están ordenados por filas y por columnas. La dimensión de una matriz es m x n, siendo m el número de filas y n el número de columnas. Cuando m = n, se dice que la matriz es una matriz cuadrada de dimensión m. Ejemplo de una matriz: Esta matriz tiene 3 filas y 3 columnas. Por tanto, es una...Área de coñecementoContexto educativo -
Fractales
 Fractales Los fractales son objetos geométricos cuya estructura se repite a diferentes escalas. En esta página mostraremos imágenes de algunos de los fractales más conocidos. 1. Fractales autosemejantes Alfombra de Sierpinski Triángulo de Sierpinski Curva de Koch Árbol binario Dragón de Heighway Árbol de Pitágoras 2. Conjunto de Mandelbrot 3. Conjunto de Julia Lleno Más información sobre fractales: Dimensión de semejanza Conjunto de Can...Área de coñecemento
Fractales Los fractales son objetos geométricos cuya estructura se repite a diferentes escalas. En esta página mostraremos imágenes de algunos de los fractales más conocidos. 1. Fractales autosemejantes Alfombra de Sierpinski Triángulo de Sierpinski Curva de Koch Árbol binario Dragón de Heighway Árbol de Pitágoras 2. Conjunto de Mandelbrot 3. Conjunto de Julia Lleno Más información sobre fractales: Dimensión de semejanza Conjunto de Can...Área de coñecemento -
Integration by U-substitution
 Integration by U-substitution method When the integrand is formed by a product (or a division, which we can treat like a product) it's recommended the use of the method known as integration by u-substitution, that consists in applying the following formula: Even though it's a simple formula, it has to be applied correctly. Let's see a few tips on how to apply it well: 1. Select u and dv correctly: as a rule, we will call u all powers and logarithms; and dv exponentials, fractions and...Área de coñecementoContexto educativo
Integration by U-substitution method When the integrand is formed by a product (or a division, which we can treat like a product) it's recommended the use of the method known as integration by u-substitution, that consists in applying the following formula: Even though it's a simple formula, it has to be applied correctly. Let's see a few tips on how to apply it well: 1. Select u and dv correctly: as a rule, we will call u all powers and logarithms; and dv exponentials, fractions and...Área de coñecementoContexto educativo -
Exponential Equations
 Exponential Equations An exponential equation is one that has exponential expressions, in other words, powers that have in their exponent expressions with the unknown factor x. For example: We will resolve some exponential equations without using logarithms. This method of resolution consists in reaching an equality of the exponentials with the same base in order to equal the exponents. Examples Example 1: Taking into account that we can write 16 as a power we can rewrite the equ...Área de coñecementoContexto educativo
Exponential Equations An exponential equation is one that has exponential expressions, in other words, powers that have in their exponent expressions with the unknown factor x. For example: We will resolve some exponential equations without using logarithms. This method of resolution consists in reaching an equality of the exponentials with the same base in order to equal the exponents. Examples Example 1: Taking into account that we can write 16 as a power we can rewrite the equ...Área de coñecementoContexto educativo -
Inecuaciones
 Una inecuación es una relación de desigualdad entre dos expresiones algebraicas en las que aparece una o más incógnitas. Resolver una inecuación consiste en encontrar todos los valores de la incógnita para los que se cumple la relación de desigualdad. Los signos de desigualdad que se utilizan en las inecuaciones son: <, >, ≤ y ≥: a < b significa "a es menor estrictamente que b". Por ejemplo: 2 < 3. a > b significa "a es mayor estrictamente que b". Por ejemplo: 3 >...Área de coñecementoContexto educativo
Una inecuación es una relación de desigualdad entre dos expresiones algebraicas en las que aparece una o más incógnitas. Resolver una inecuación consiste en encontrar todos los valores de la incógnita para los que se cumple la relación de desigualdad. Los signos de desigualdad que se utilizan en las inecuaciones son: <, >, ≤ y ≥: a < b significa "a es menor estrictamente que b". Por ejemplo: 2 < 3. a > b significa "a es mayor estrictamente que b". Por ejemplo: 3 >...Área de coñecementoContexto educativo -
Portafolio docente y educativo INTEF Grupo B1
 En este eportafolio quiero reflejar los aspectos más importantes de la docencia en la ESO y Bachillerato, tal y como yo la entiendo. El portafolio se clasifica en los aspectos básicos de un portafolio: perfil personal y docente, filosofía docente, materiales y su uso y evaluación. Este portafolio es un proyecto recien creado que se irá actualizando y creciendo con mis aportaciones y las de los alumnos y, sobre todo, con críticas y autocríticas constructivas que me ayuden mejorar la práctica...Área de coñecementoContexto educativo
En este eportafolio quiero reflejar los aspectos más importantes de la docencia en la ESO y Bachillerato, tal y como yo la entiendo. El portafolio se clasifica en los aspectos básicos de un portafolio: perfil personal y docente, filosofía docente, materiales y su uso y evaluación. Este portafolio es un proyecto recien creado que se irá actualizando y creciendo con mis aportaciones y las de los alumnos y, sobre todo, con críticas y autocríticas constructivas que me ayuden mejorar la práctica...Área de coñecementoContexto educativo -
Ecuaciones logarítmicas y sistemas
 Una ecuación logarítmica es aquella en la que la incógnita se encuentra en el argumento de logaritmos. Su resolución se reduce, en realidad, a la resolución de ecuaciones del mismo tipo que las expresiones de los argumentos (ecuaciones de segundo grado, tercer grado, irracionales...) Normalmente, si en logaritmos no se especifica la base, supondremos que es 10. Para resolver este tipo de ecuaciones se necesita conocer las propiedades de los logaritmos: Propiedades de los logaritmos Logari...Área de coñecementoContexto educativo
Una ecuación logarítmica es aquella en la que la incógnita se encuentra en el argumento de logaritmos. Su resolución se reduce, en realidad, a la resolución de ecuaciones del mismo tipo que las expresiones de los argumentos (ecuaciones de segundo grado, tercer grado, irracionales...) Normalmente, si en logaritmos no se especifica la base, supondremos que es 10. Para resolver este tipo de ecuaciones se necesita conocer las propiedades de los logaritmos: Propiedades de los logaritmos Logari...Área de coñecementoContexto educativo


