Una vez leída la información sobre el Grupo de isometrías de los rosetones, a la que se puede acceder desde la misma página, en la escena se explora la clase de losDiedros (*n, nm), la segunda de las dos clases de rosetones, realizando las construcciones indicadas o mediante diseños libres de azulejos. Es recomendable realizar antes de esta la actividad sobre la otra clase de rosetones, la de los rosetones Cíclicos.

Una vez leída la información sobre el Grupo de isometrías de los rosetones, a la que se puede acceder desde la misma página, en la escena se explora la clase de los Cíclicos (n, n), la primera de las dos clases de rosetones, realizando las construcciones indicadas o mediante diseños libres de azulejos.

Esta actividad te permitirá demostrar tu habilidad para encontrar el grupo de isometrías correspondiente a un mosaico. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Es aconsejable realizar primero las actividades planteadas en la aplicación de esta misma colección llamada "Prácticas de exploración de mosaicos". Se incluyen las soluciones de las actividades propuestas.

Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. En esta actividad se puede crear un diseño propio de un mosaico. Para ello primero hay que elegir el grupo de isometrías, situar los vértices del azulejo que se repite por traslación y dibujar el motivo decorativo en la región sombreada.

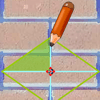Esta actividad te permitirá practicar el procedimiento para averiguar a qué grupo de isometrías corresponde un mosaico cualquiera. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Las actividades propuestas se comprueban con su propia autoevaluación.

Esta actividad te permitirá explorar un mosaico periódico cualquiera y averiguar a qué grupo de isometrías corresponde. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Es aconsejable realizar primero las actividades planteadas en la aplicación de esta misma colección llamada "Prácticas de exploración de mosaicos". Las actividades propuestas se comprueban con su propia autoevaluación.

En esta actividad explorarás el último grupo de isometrías, el grupo 17 (*632, p6m). Es el último de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de diamante. Se incluye las soluciones de las actividades propuestas.

En esta actividad explorarás el grupo 16 (632, p6). Es el cuarto de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de diamante. Se incluye las soluciones de las actividades propuestas.

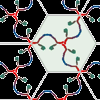En esta actividad explorarás el grupo 15 (3*3, p31m). Es el tercero de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de diamante. Se incluye las soluciones de las actividades propuestas.

En esta actividad explorarás el grupo 14 (*333, p3m1). Es el segundo de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de diamante. Se incluye las soluciones de las actividades propuestas.

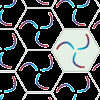En esta actividad explorarás el grupo 13 (333, p3). Es el primero de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de diamante. Se incluye las soluciones de las actividades propuestas.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta primera actividad se explora el grupo 11 (*442, p4m). Es el segundo de los tres grupos de mosaicos que se pueden crear con azulejos con forma de cuadrado.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta primera actividad se explora el grupo 10 (442, p4). Es el primero de los tres grupos de mosaicos que se pueden crear con azulejos con forma de cuadrado.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 9 (22*, pmg). Es el último de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de rectángulo.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 8 (22x, pgg). Es el cuarto de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de rectángulo

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 7 (*2222, pmm). Es el tercero de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de rectángulo.

Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 6 (xx, pg). Es el segundo de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de rectángulo.

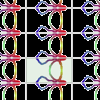Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 5 (**, pm). Es el primero de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de rectángulo.

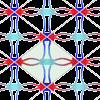Antes de empezar con los mosaicos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. Es recomendable seguir el orden numérico de los grupos. En esta actividad se explora el grupo 4 (2*22, cmm). Es el segundo de los dos grupos de mosaicos que se pueden crear con azulejos con forma de rombo.

En la escena se pueden observar y manipular ejemplos de los cuatro tipos de isometrías y conocer sus principales características: Traslación, Rotación o Giro, Reflexión o Simetría axial y Reflexión Desplazada.