Polígonos I Un polígono es una figura geométrica formada por segmentos rectos (llamados lados) unidos de forma que encierran un área en el plano. Ejemplos: polígonos de cinco lados (pentágonos) Estos polígonos se denominan pentágonos puesto que tienen cinco lados. Un polígono es regular cuando todos sus lados tienen la misma longitud y los ángulos (interiores) que forman los lados son iguales. Si no es así, el polígono es irregular. Ejemplo: polígonos regulares El nombre de un políg...

Proporcionalidad compuesta En los problemas de proporcionalidad compuesta intervienen tres variables, siendo una de ellas la variable incógnita. La relación entre las variables con la variable incógnita puede ser una proporcionalidad directa o inversa. Se resuelven aplicando una regla de tres compuesta. Método de resolución Explicaremos el método a medida que resolvemos el siguiente problema: Problema: si 6 niños comen 160 caramelos en 2 horas, ¿cuántas horas tardan 3 niños en comer 120 ...

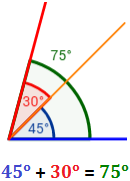
Un ángulo es la región del plano comprendida entre dos semirrectas con origen común:  Si dividimos una circunferencia en 360 partes iguales, un grado sexagesimal es una de estas partes. Un grado se expresa como 1º:  Para medir un ángulo, éste se coloca sobre el diagrama anterior: Al colocar el ángulo rojo sobre la circunferencia observamos que éste mide 30º (30 grados sexagesimales). Minutos y segundos sexagesimales Si dividimos un grado sexagesimal en 60 partes iguales, cada una...

Este REA que he encontrado sobre folclore en España es adecuado para todos los niveles de Música de la ESO y de las asignatura de Historia de la Música de 2º de Bachillerato. También puede ser adecuado para trabajar en Geografía e Historia de la ESO, ya que alude a la expresión del folclore en toda España, Educación de Adultos, en las Enseñanzas Profesionales de Música y Danza y como Formación del Profesorado. Este REA ha sido creado porManuel Gértrudix Barrio, Felipe Gértrudix Barrio y Felip...

Equacions exponencials i logarítmiques 1. Equacions exponencials Una equació exponencial és aquella en la que apareixen exponencials, és a dir, potències que tenen la incògnita, x, en els exponents. En aquesta pàgina resoldrem equacions exponencials sense emprar logaritmes. El mètode de resolució consisteix en aconseguir una igualtat entre dues exponencials amb la mateixa base per poder igualar els seus exponents. Aplicarem les propietats de les potències. Exemple 1: Si escrivim 27 com...

Equacions de segon grau completes i incompletes Una equació de segon grau és una equació polinòmica de grau 2, és a dir, el major grau dels monomis és 2, o siga, x al quadrat. Com que l'equació és de grau 2, tindrà, com a molt, dues arrels (solucions) distintes. Tota equació de segon grau es pot escriure en la forma Si ningun dels coeficients, a,b i c és zero, és a dir, direm que l'equació és completa. Si no és així (si b ó c és 0), direm que és incompleta. 1. Equació completa Les...

Una ecuación irracional es aquella en la que aparecen raíces que contienen a la incógnita, es decir, la incógnita se encuentra bajo signos radicales. Para resolver una ecuación irracional, se elevan ambos lados de la ecuación al orden de la raíz (al cuadrado, al cubo...). Este procedimiento aumenta el grado de la ecuación, por lo que posiblemente estamos añadiendo soluciones. Es por ello por lo que siempre comprobaremos las soluciones. Otro problema que conlleva esta potenciación, en el cas...

Si conocemos dos lados de un triángulo rectángulo, podemos calcular el otro lado aplicando el teorema de Pitágoras. Sin embargo, en ocasiones no conocemos dos lados, pero sí conocemos uno de los otros dos ángulos no rectos. En estos casos es cuando utilizamos el seno y el coseno. El coseno de un ángulo α se define como el cociente del lado contiguo al ángulo α y la hipotenusa. De forma análoga, el seno de α se define como el cociente del lado opuesto al ángulo α y la hipotenusa. Nota: si...

Intervalos Definimos el intervalo [a,b] siendo a<b como el conjunto formado por todos los números (reales) que son mayores o iguales que a y menores o iguales que b. Los números a y b se denominan extremos del intervalo [a,b]. Representación en la recta real del intervalo [a,b]: Ejemplos: El número 3 está en el intervalo [0,5] porque 3 es mayor o igual que 0 y menor o igual que 5. El número 6 no está en el intervalo [0,5] porque es mayor o igual que 0 pero no es menor o ...

Ecuaciones Exponenciales Una ecuación exponencial es aquella en la que aparecen exponenciales, es decir, potencias cuyos exponentes son expresiones en las que aparece la incógnita, x. En esta sección, resolveremos ecuaciones exponenciales sin usar logaritmos. El método de resolución consiste en conseguir una igualdad de exponenciales con la misma base para poder igualar los exponentes. Para ello, utilizaremos las propiedades de las potencias. Ejemplo 1: Escribimos 16 como una potencia ...

Logarithmic Equations and Systems A logarithmic equation is an equation that has an unknown factor in the argument of a logarithm. In reality, the resolution is reduced to the resolution of equations of the same type as the expressions in the arguments (quadratic equations, cubic equations, irrational equations...). Before starting the exercises, let's remember the logarithmic properties: Logarithm of a product: Logarithm of a quotient: Logarithm of a power: Change of base: Use...

Pythagoren Theorem Pythagoras' Theorem: Given a right triangle with sides a and b and a hypotenuse h (the side opposite the right angle). Then, Remember that... triangle is a right-angled triangle because it has a right angle, an angle of 90º or π / 2 radians The hypotenuse is the opposite side as the right angle. Note: h is always bigger than the other sides, as shows h > a and h > b. The Pythagoras theorem is one of the most known results in mathematics and also one...

URL: http://eduteka.icesi.edu.co/post/6 ESTRUCTURA Y ORGANIZACIÓN: El recurso tiene claramente explicados los objetivos, estándares de aprendizaje y competencias que se desarrollan. Del mismo modo las tareas a desarrollar por los alumnos son claras y concisas, así como el modo de evaluar la actividad. APLICACIÓN EN EL AULA: Es fácil de aplicar en el aula de informática ya que los contenidos se presentan a los alumnos mediante una animación. ELEMENTOS DE DISEÑO: La actividad se basa ...

Movimiento Rectilíneo Uniformemente Acelerado El movimiento rectilíneo uniformemente acelerado (MRUA) o movimiento rectilíneo uniformemente variado (MRUV) es un movimiento cuya trayectoria es una recta, pero la velocidad no es necesariamente constante porque existe una aceleración. La ecuación de la posición del móvil en el instante t en un MRUA es siendo x0 la posición inicial, v0 la velocidad inicial, a la aceleración y t el tiempo que dura el movimiento. La gráfica de la posición en ...

Una progresión (o sucesión) numérica es un conjunto de números ordenados. A cada uno de estos números los llamamos términos de la sucesión. Por ejemplo, la sucesión de los números pares es 2, 4, 6, 8, 10, 12, ... Esta sucesión está formada por infinitos términos. Algunas características de las progresiones son: En función del número que tengan, las sucesiones pueden ser finitas o infinitas. Son crecientes si cada término es mayor que su anterior y es decreciente si cada término ...

Mínim comú múltiple i màxim comú divisor 1. Descomposició de nombres Per a calcular el mínim comú múltiple o el màxim comú divisor de dos o més nombres cal descompondre aquests com un producte de potències de nombres primers. Exemple: Per descompondre un nombre dividim el nombre successivament entre nombres primers fins obtenir un 1. Més concretament: Dividim successivament per nombres primers (de manera que la divisió sigui exacta). La descomposició és el producte de les potències d...

Teorema de Pitàgores Teorema i exemples d'aplicació. 1. Teorema de Pitàgores Donat un triangle rectangle amb catets a i b i hipotenusa h (el costat oposat a l'angle recte). Aleshores, Recordem que: el triangle és rectangle perquè té un angle recte, és a dir, un angle de 90 graus ó π / 2 radiants. la hipotenusa és el costat oposat a l'angle recte Problemes d'aplicació Problema 1 Calcular la hipotenusa del triangle rectangle de costats 3cm i 4cm. Solució: Els costats só...

Proporcionalidad directa Dos magnitudes a y b son directamente proporcionales cuando existe una constante k tal que a/b = k La constante k se denomina constante de proporcionalidad o razón. Se dice que a y b mantienen una relación de proporcionalidad directa. En la proporcionalidad directa, cuando una de las magnitudes cambia, la otra también debe hacerlo de modo que su razón se mantenga constante. Ejemplo: En un movimiento con velocidad constante v, la distancia recorrida viene dada p...

Mi Ple