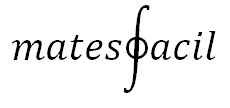
El sistema decimal es un sistema de numeración posicional. Cuando nos enseñan los números por primera vez, éste es el sistema que se emplea y sin duda es el que más se usa en matemáticas. Sin embargo, hay otros sistemas de numeración que, debido a sus aplicaciones prácticas, también son importantes. Tal es el caso del sistema octal, que se utiliza a veces en informática. Los símbolos que se usan en este sistema son: 0, 1, 2, 3, 4, 5, 6, 7 Cambio de base 10 a base 8 Veamos el método para p...

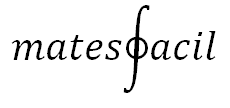
El sistema hexadecimal es un sistema de numeración posicional de base 16. Los símbolos que se usan en este sistema son: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Cambio de base 10 a base 16 Veamos el método para pasar del sistema decimal al sistema hexadecimal mediante un ejemplo. Escribiremos el número 460 (base 10) en base 16: Dividimos el número entre 16: Si el cociente es mayor o igual que 16, lo dividimos entre 16. En nuestro caso, el cociente es 28 (mayor que 1...

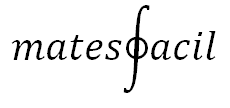
Una ecuación irracional es aquella en la que aparecen raíces que contienen a la incógnita, es decir, la incógnita se encuentra bajo signos radicales. Para resolver una ecuación irracional, se elevan ambos lados de la ecuación al orden de la raíz (al cuadrado, al cubo...). Este procedimiento aumenta el grado de la ecuación, por lo que posiblemente estamos añadiendo soluciones. Es por ello por lo que siempre comprobaremos las soluciones. Otro problema que conlleva esta potenciación, en el cas...

Juan José de Haro presenta en el Observatorio de Tecnología Educativa TiddlyWiki, herramienta que permite organizar la información para acceder a ella con facilidad y rapidez. Una de las ventajas que aporta TiddlyWiki es la gran portabilidad que nos ofrece, ya que permite acceder a dicha información de forma local o a través de Internet. El archivo creado es un HTML, que puede ser visualizado por cualquier navegador. Este archivo permite añadir elementos para organizar contenidos complejos, ...

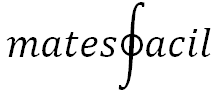
Estudio de la continuidad, monotonía, existencia de extremos (máximos y mínimos) y curvatura (convexa o cóncava). (aplicaciones del cálculo diferencial) Estudio de la función: 1. Dominio, recorrido y continuidad: Como la función es una raíz cuadrada, el radicande debe ser mayor o igual que 0. Resolvemos la inecuación: La desigualdad siempre se cumple ya que la ecuación de segundo grado no tiene soluciones (reales) y, por tanto, la función no cambia de signo, manteniéndose siempre en...

Dominio y recorrido de una función 1. Dominio y codominio Una función, f, es una ley entre dos conjuntos de números: el dominio y el codominio. A cada número del dominio le hace corresponder un único número del codominio. Esta ley es una correspondencia unívoca. Ejemplo: En el ejemplo, el dominio es el conjunto El codominio es el conjunto La expresión de la función es ya que lo que hace la función es multiplicar por dos cada número del dominio. Podemos observar cómo a cada ele...

Matrices y Sistemas de Ecuaciones Lineales (SEL) 1. Definición de SEL y su solución Un sistema de m ecuaciones lineales con n incógnitas (SEL) y coeficientes en un cuerpo K (como los reales o los complejos) es A los elementos ai,j se les denomina coeficientes del SEL y a los b_i términos independientes. Un ejemplo de un SEL de dos ecuaciones y dos incógnitas es Dimensión del SEL: dimensión cuadrada: si m = n (tiene el mismo número de ecuaciones que de incógnitas). dimensión...

En este artículo vamos a obtener una fórmula para calcular la derivada de una función elevada a otra función, por ejemplo: 1. La fórmula Sea la función y(x) la que queremos derivar. Supongamos que es de la forma: Es decir, la función y(x) es la función f(x) elevada a la función g(x). Para facilitar la notación, escribimos y, f y g para referirnos a las funciones y(x), f(x) y g(x), respectivamente. Las derivadas de estas funciones las escribiremos como y', f' y g'. Por tanto, la funci...

Desde hoy está abierta la inscripción para la 2ª edición del Mooc: Uso educativo de la narración digital. (#EduNarraMooc). Este es su video de presentación: Podéis inscribiros desde aquí: http://mooc.educalab.es/courses/INTEF/INTEF161/2016_ED2/about No os llevará más de un minuto. Tenéis más información sobre este mooc en este post del blog del INTEF. Os animo no sólo a particpar en el mooc, también a darle difusión entre vuestros contactos y redes sociales ¡gracias! ¡Seguimos!

Os presento el proyecto colaborativo Tertulias con sabor a chocolate “una iniciativa centrada en la comunicación oral, en el diálogo, en la palabra sentida, imaginada, pensada, en la palabra que encuentra oportunidad y espacio para ser hablada y escuchada, en la palabra que, adentrándose en el universo del otro, va tejiendo respuesta...” en la que “...resuena la tradición de las comunidades de investigación fIlosófica, de las comunidades de aprendizaje, de las comunidades dialógicas” (1) Es ...

¿Qué significa ser competente en matemáticas, ciencia y tecnología? ¿Tiene sentido considerar una única competencia que abarque tres áreas distintas? ¿Cómo pueden los escolares desarrollarla? ¿Qué estrategias, recursos y herramientas puede usar el profesorado para evaluarla? Todas estas cuestiones y otras muchas las abordamos en #STEMooc, cuyas inscripciones ya están abiertas. Comienzo de la primera edición del MOOC: 8 de febrero de 2016. Información e inscripción enhttp://mooc.educalab.es/...

La pizarra digital interactiva PDI es un instrumento didáctico con múltiples posibilidades y opciones. Mi experiencia es que puede utilizarse como único recurso TIC en clase pero también complementada con tablets, dispositivos móviles o portátiles. En todas las situaciones el eje fundamental es la PDI. Todos los recursos en: PqA