PROCOMÚN
Showing results from 1 to 20 out of 572
-
Las Gimnospermas
 Unidad didáctica sobre las Gimnospermas Biología y Geología 1º ESO 12-13 añosUnidad didáctica sobre las GimnospermasTipo de recurso
Unidad didáctica sobre las Gimnospermas Biología y Geología 1º ESO 12-13 añosUnidad didáctica sobre las GimnospermasTipo de recurso -
Calculadora de límites de funciones
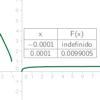 La forma más sencilla de averiguar aproximadamente a qué valor se aproxima una función F cuando x se acerca a un valor determinado c, consiste simplemente en averiguar el valor de la función para valores muy próximos a c, como F(c + 0.0001) o como F(c - 0.0001). Pero a veces el cálculo del límite es solo una operación intermedia, por lo que necesitamos valores exactos, no aproximados. Esta actividad es una herramienta útil para el cálculo de límites de funciones.Área de conocimientoTipo de recursoCollections
La forma más sencilla de averiguar aproximadamente a qué valor se aproxima una función F cuando x se acerca a un valor determinado c, consiste simplemente en averiguar el valor de la función para valores muy próximos a c, como F(c + 0.0001) o como F(c - 0.0001). Pero a veces el cálculo del límite es solo una operación intermedia, por lo que necesitamos valores exactos, no aproximados. Esta actividad es una herramienta útil para el cálculo de límites de funciones.Área de conocimientoTipo de recursoCollections -
Límites laterales y continuidad: I. Límite por la izquierda
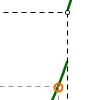 En esta actividad veremos qué significado tiene el límite por la izquierda de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.Área de conocimientoTipo de recursoCollections
En esta actividad veremos qué significado tiene el límite por la izquierda de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.Área de conocimientoTipo de recursoCollections -
Límites laterales y continuidad: II. Límite por la derecha
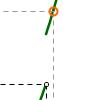 En esta actividad veremos qué significado tiene el límite por la derecha de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.Área de conocimientoTipo de recursoCollections
En esta actividad veremos qué significado tiene el límite por la derecha de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.Área de conocimientoTipo de recursoCollections -
Límites laterales y continuidad: III. Continuidad
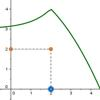 En esta actividad veremos qué significado tiene el límite de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.Área de conocimientoTipo de recursoCollections
En esta actividad veremos qué significado tiene el límite de una función en un punto, mediante un ejemplo concreto, en donde el punto en el que se definirá el límite es c = 2. Esta definición de límite de la función en un punto es esencial para definir la continuidad en ese punto.Área de conocimientoTipo de recursoCollections -
Lados curvos
 El objetivo en esta actividad es averiguar cómo se forman figuras complejas alterando algunos elementos de figuras sencillas, como polígonos regulares y circunferencias.Área de conocimientoTipo de recursoCollections
El objetivo en esta actividad es averiguar cómo se forman figuras complejas alterando algunos elementos de figuras sencillas, como polígonos regulares y circunferencias.Área de conocimientoTipo de recursoCollections -
Simetría rotacional
 En esta actividad se practica con simetrías rotacionales. Decimos que una figura plana tiene simetría rotacional cuando podemos encontrar un centro (llamado centro de rotación) de manera que si giramos la figura completa un cierto ángulo (mayor o igual a 0º y menor que 360º), la figura rotada coincide con la figura original. Cuando un figura tiene simetría rotacional, a cada punto le corresponden otro punto (que se llama "punto rotado" o "imagen") a la misma distancia del centro, de forma que...Área de conocimientoTipo de recursoCollections
En esta actividad se practica con simetrías rotacionales. Decimos que una figura plana tiene simetría rotacional cuando podemos encontrar un centro (llamado centro de rotación) de manera que si giramos la figura completa un cierto ángulo (mayor o igual a 0º y menor que 360º), la figura rotada coincide con la figura original. Cuando un figura tiene simetría rotacional, a cada punto le corresponden otro punto (que se llama "punto rotado" o "imagen") a la misma distancia del centro, de forma que...Área de conocimientoTipo de recursoCollections -
Billar
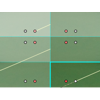 En esta actividad mediante el juego del billar se practican diversos ejemplos de simetrías axiales.Área de conocimientoTipo de recursoCollections
En esta actividad mediante el juego del billar se practican diversos ejemplos de simetrías axiales.Área de conocimientoTipo de recursoCollections -
Espirales
 Se trata de utilizar una construcción de Geogebra en la que aparecen figuras reales, piñas y girasoles, y sobre ellas se dibujan espirales y se cuenta el número de espirales en uno u otro sentido, observando que coincide siempre con dos términos consecutivos de la sucesión de Fibonacci.Área de conocimientoTipo de recursoCollections
Se trata de utilizar una construcción de Geogebra en la que aparecen figuras reales, piñas y girasoles, y sobre ellas se dibujan espirales y se cuenta el número de espirales en uno u otro sentido, observando que coincide siempre con dos términos consecutivos de la sucesión de Fibonacci.Área de conocimientoTipo de recursoCollections -
Copa
 Solemos infravalorar la longitud de la circunferencia, pues tomamos como referencia el diámetro, olvidándonos que la longitud real es aproximadamente 3 veces ( pi veces) el diámetro. Objeto digital educativo que formula cuestiones relacionadas con el diámetro de la circunferencia descrita por el borde de una copa y la altura de esta. La aplicación incluye autoevaluación.Tipo de recursoCollections
Solemos infravalorar la longitud de la circunferencia, pues tomamos como referencia el diámetro, olvidándonos que la longitud real es aproximadamente 3 veces ( pi veces) el diámetro. Objeto digital educativo que formula cuestiones relacionadas con el diámetro de la circunferencia descrita por el borde de una copa y la altura de esta. La aplicación incluye autoevaluación.Tipo de recursoCollections -
Tamaño aparente de la luna y del sol
 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta actividad podrás comprobar cómo con la simple observación directa, sin sofisticados instrumentos, Aristarco consiguió medir el tamaño aparente de la Luna y Sol en el cielo, es decir, determinar el valor del ángulo con el que los vemos.Área de conocimientoTipo de recursoCollections
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta actividad podrás comprobar cómo con la simple observación directa, sin sofisticados instrumentos, Aristarco consiguió medir el tamaño aparente de la Luna y Sol en el cielo, es decir, determinar el valor del ángulo con el que los vemos.Área de conocimientoTipo de recursoCollections -
Ángulos entre paralelas
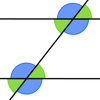 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Cuando dos rectas paralelas son cortadas por otra recta, a la que llamaremos transversal se forman 8 ángulos. Esos ocho ángulos guardan una estrecha relación entre sí, de modo que en cuanto conocemos uno de ellos podemos averiguar lo que valen los demás. En esta aplicación vamos a descubrir estas relacion...Área de conocimientoTipo de recursoCollections
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. Cuando dos rectas paralelas son cortadas por otra recta, a la que llamaremos transversal se forman 8 ángulos. Esos ocho ángulos guardan una estrecha relación entre sí, de modo que en cuanto conocemos uno de ellos podemos averiguar lo que valen los demás. En esta aplicación vamos a descubrir estas relacion...Área de conocimientoTipo de recursoCollections -
Reloj
 En esta aplicación verás un reloj analógico y dos digitales. Podrás escoger libremente la hora que quieras en cada momento, y mover los deslizadores para ver los cambios correspondientes. También puedes sincronizar los relojes con la hora del ordenador. Podrás observar las notaciones en que está expresado el tiempo, así como los ángulos que forman las agujas horaria y minutero.Tipo de recursoCollections
En esta aplicación verás un reloj analógico y dos digitales. Podrás escoger libremente la hora que quieras en cada momento, y mover los deslizadores para ver los cambios correspondientes. También puedes sincronizar los relojes con la hora del ordenador. Podrás observar las notaciones en que está expresado el tiempo, así como los ángulos que forman las agujas horaria y minutero.Tipo de recursoCollections -
Balanza (naturales)
 Este objeto educativo forma parte del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creado utilizando el applet de Geogebra, simula una balanza en la que el contenido de cada uno de los platillos se corresponde con uno de los miembros de una ecuación. Para resolver dicha ecuación hay que reducir el contenido de los platillos tanto como se pueda, manteniendo en todo momento el equilibrio.Área de conocimientoTipo de recursoCollections
Este objeto educativo forma parte del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creado utilizando el applet de Geogebra, simula una balanza en la que el contenido de cada uno de los platillos se corresponde con uno de los miembros de una ecuación. Para resolver dicha ecuación hay que reducir el contenido de los platillos tanto como se pueda, manteniendo en todo momento el equilibrio.Área de conocimientoTipo de recursoCollections -
Balanza (enteros)
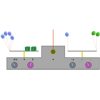 Este objeto educativo forma parte del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creado utilizando el applet de Geogebra, simula una balanza en la que el contenido de cada uno de los platillos se corresponde con uno de los miembros de una ecuación. Para resolver dicha ecuación hay que reducir el contenido de los platillos tanto como se pueda, manteniendo en todo momento el equilibrio.Área de conocimientoTipo de recursoCollections
Este objeto educativo forma parte del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creado utilizando el applet de Geogebra, simula una balanza en la que el contenido de cada uno de los platillos se corresponde con uno de los miembros de una ecuación. Para resolver dicha ecuación hay que reducir el contenido de los platillos tanto como se pueda, manteniendo en todo momento el equilibrio.Área de conocimientoTipo de recursoCollections -
Fracciones (propias): multiplica y divide
 Este es uno de los objetos educativos del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creado utilizando el applet de Geogebra, proporciona una interpretación gráfica de la multiplicación y la división de fracciones propias.Tipo de recursoCollections
Este es uno de los objetos educativos del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creado utilizando el applet de Geogebra, proporciona una interpretación gráfica de la multiplicación y la división de fracciones propias.Tipo de recursoCollections -
El monosabio
 Este es uno de los objetos educativos del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra, esta aplicación simula un antiguo juguete educativo, que calcula el producto de dos números y el cuadrado de un número.Tipo de recursoCollections
Este es uno de los objetos educativos del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra, esta aplicación simula un antiguo juguete educativo, que calcula el producto de dos números y el cuadrado de un número.Tipo de recursoCollections -
Áreas
 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra, esta aplicación muestra un ejemplo sobre la necesidad de comprobar la exactitud de nuestras observaciones, la forma de percibir un cuerpo y, si es posible, incluso hallar una explicación razonada de lo que vemos. En este ejemplo: Mueve el punto hasta que creas que las áreas de las superficies visibles d...Área de conocimientoTipo de recursoCollections
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra, esta aplicación muestra un ejemplo sobre la necesidad de comprobar la exactitud de nuestras observaciones, la forma de percibir un cuerpo y, si es posible, incluso hallar una explicación razonada de lo que vemos. En este ejemplo: Mueve el punto hasta que creas que las áreas de las superficies visibles d...Área de conocimientoTipo de recursoCollections -
La diagonal del cuadrado
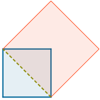 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta aplicación podrás aprender un procedimiento para calcular la longitud exacta de la diagonal de un cuadrado conociendo la longitud de su lado, y viceversa, así como las áreas del cuadrado y del de lado la diagonal.Área de conocimientoTipo de recursoCollections
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta aplicación podrás aprender un procedimiento para calcular la longitud exacta de la diagonal de un cuadrado conociendo la longitud de su lado, y viceversa, así como las áreas del cuadrado y del de lado la diagonal.Área de conocimientoTipo de recursoCollections -
Azulejos
 Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta aplicación analizaremos el concepto de área y perímetro de figuras que iremos construyendo adosando azulejos cuadrados de 1 centímetro de lado.Área de conocimientoTipo de recursoCollections
Este es un objeto educativo del Proyecto Gauss, desarrollado por el ITE para su utilización en una pizarra digital y en los ordenadores del alumnado. Creada utilizando el applet de Geogebra. En esta aplicación analizaremos el concepto de área y perímetro de figuras que iremos construyendo adosando azulejos cuadrados de 1 centímetro de lado.Área de conocimientoTipo de recursoCollections


