PROCOMÚN
Showing results from 81 to 100 out of 255
-
Cálculo de áreas. Representación digital.
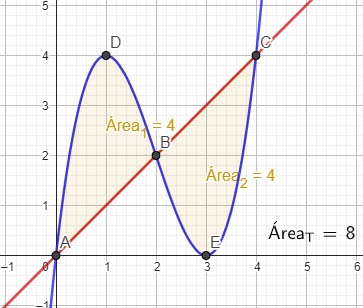 El alumno se adentra con esta práctica en el aprendizaje de aplicaciones matemáticas para el cálculo de áreas y su representación en formato digital.Área de conocimientoContexto educativoTipo de recurso
El alumno se adentra con esta práctica en el aprendizaje de aplicaciones matemáticas para el cálculo de áreas y su representación en formato digital.Área de conocimientoContexto educativoTipo de recurso -
Descubriendo las medidas de la ciudad
 SdA que pretende emplear los conocimientos y destrezas adquiridos de Trigonometría, para resolver retos matemáticos en torno a una gincana matemática en el casco histórico de la ciudad de Córdoba. También se quiere sensibilizar y dar a conocer el patrimonio histórico-artístico de la ciudad. Igualmente se pretende crear materiales que permitan difundir en distintos formatos los conocimientos adquiridos.Área de conocimientoContexto educativoTipo de recurso
SdA que pretende emplear los conocimientos y destrezas adquiridos de Trigonometría, para resolver retos matemáticos en torno a una gincana matemática en el casco histórico de la ciudad de Córdoba. También se quiere sensibilizar y dar a conocer el patrimonio histórico-artístico de la ciudad. Igualmente se pretende crear materiales que permitan difundir en distintos formatos los conocimientos adquiridos.Área de conocimientoContexto educativoTipo de recurso -
SdA. Nochebuena con fracciones
 - Temática: Fracciones - Curso: 1º ESO - Asignatura: Matemáticas - Temporalización: Última Situación de Aprendizaje de la primera evaluación. 12 sesiones - Idioma: CastellanoÁrea de conocimientoContexto educativoTipo de recurso
- Temática: Fracciones - Curso: 1º ESO - Asignatura: Matemáticas - Temporalización: Última Situación de Aprendizaje de la primera evaluación. 12 sesiones - Idioma: CastellanoÁrea de conocimientoContexto educativoTipo de recurso -
ARTEMÁTICA
 ABP centrado en el conocimiento y estudio de estilos pictóricos, a través de la digitalización, el arte, las matemáticas y otras disciplinas.Área de conocimientoContexto educativoTipo de recurso
ABP centrado en el conocimiento y estudio de estilos pictóricos, a través de la digitalización, el arte, las matemáticas y otras disciplinas.Área de conocimientoContexto educativoTipo de recurso -
Geometría 1º ESO
Recursos hechos con Geogebra para trabajar aspectos geométricos en 1º ESO Se recomienda realizar las actividades siguiendo el orden del itinerarioÁrea de conocimientoContexto educativo -
Un paseo por la Alhambra
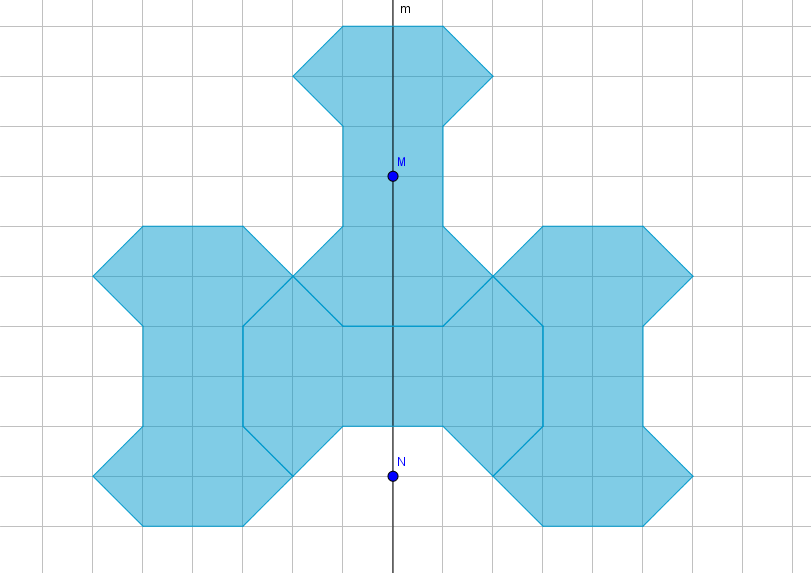 Hola a todos: Estoy muy contenta de poder compartir mi primer Proyecto Flipped Classroom. Estoy muy orgullosa de él porque me ha costado mucho aprender a utilizar todas las herramientas empleadas y sobre todo ponerme las pilas con las TIC. Espero que a alguien le sea útil. Un paseo por la AlhambraÁrea de conocimientoContexto educativo
Hola a todos: Estoy muy contenta de poder compartir mi primer Proyecto Flipped Classroom. Estoy muy orgullosa de él porque me ha costado mucho aprender a utilizar todas las herramientas empleadas y sobre todo ponerme las pilas con las TIC. Espero que a alguien le sea útil. Un paseo por la AlhambraÁrea de conocimientoContexto educativo -
Analisis REA: "El área de las figuras planas"
El recurso seleccionado para elaborar el análisis lleva por título "El área de las figuras planas". Podréis visitarlo a través del siguiente enlace:http://procomun.educalab.es/es/ode/view/1445270077894 El recurso trata de esclarecer el origen de las fórmulas utilizadas para el cálculo de algunas áreas de figuras planas. En cuanto a la organización del recurso, está subdividida en apartados, que estructuran de manera muy clara el recurso, y ayudan a su seguimiento y desarrollo. Así mismo ci...Área de conocimientoContexto educativo -
Proyecto Flipped Classroom "Movimientos en el plano"
El proyecto realizado en el curso Flipped Classroom INTEF está dirigido a alumnos de 3º de la ESO, se realiza con una distribución del aula en grupos cooperativos y se necesita conexión a internet y ordenador personal portátil. Os dejo el enlace de la entrada del blog donde se puede encontrar el proyecto detallado (documento word). http://flippedclassroomquim.blogspot.com.es/2017/11/proyecto-final-movimientos-en-el-plano.htmlÁrea de conocimientoContexto educativo -
Cocina paramétrica con Geogebra (Carmen González Martí)
Los parámetros matemáticos tienen fama de ser indigestos en la adolescencia. Sin embargo, son un ingrediente imprescindible en toda buena cocina algebraica. Ofrecemos unos pequeños aperitivos variados para degustar en ocasiones especiales (talleres, jornadas culturales) aunque son deliciosos en cualquier momento. Dificultad: media; recomendado a partir de 3º ESO Ingredientes: - Un puñado de adolescentes - Ordenadores (aprox. uno por cabeza) - Geogebra - Tiempo (en general) Preparaci...Área de conocimientoContexto educativo -
¿Te atreves a pilotar un dron entre dos ciudades españolas que tú elijas?
Hola, buenas tardes: Aquí os comparto el enlace a mi blog con el proyecto de pilotaje de un dron entre dos ciudades españolas. Está enmarcado dentro de la asignatura de matemáticas de 1º ESO y utiliza Google Maps y Geogebra. http://pasitoapasitoconflippedclassroom.blogspot.com.es/2016/05/presentacion-proyecto-flipped-classroom.html Espero que os guste y a ver si os animáis a hacer comentarios.Área de conocimientoContexto educativo -
Mapa conceptual de mi REA: Moviendo Funciones
Mapa conceptual del Recurso Educativo Abierto: Moviendo Funciones. https://www.mindmeister.com/601847732Área de conocimientoContexto educativo -
Proyecto Gauss para Matemáticas
 ElProyecto GaussdelINTEF brinda al profesorado varios centenares de recursos de aprendizaje que cubren contenidos de matemáticas correspondientes a Primaria,Secundaria y Bachillerato. IncluyenappletsdeGeoGebrainteractivos, queofrecen a la comunidad escolar una forma diferente y creativa de enseñar y de aprender matemáticas. Están diseñados para ser utilizados tanto sobre pizarra digital como en ordenadores, y recientemente se han actualizado a html5 para garantizar su funcionalidad en cua...Área de conocimientoContexto educativo
ElProyecto GaussdelINTEF brinda al profesorado varios centenares de recursos de aprendizaje que cubren contenidos de matemáticas correspondientes a Primaria,Secundaria y Bachillerato. IncluyenappletsdeGeoGebrainteractivos, queofrecen a la comunidad escolar una forma diferente y creativa de enseñar y de aprender matemáticas. Están diseñados para ser utilizados tanto sobre pizarra digital como en ordenadores, y recientemente se han actualizado a html5 para garantizar su funcionalidad en cua...Área de conocimientoContexto educativo -
Proceso de conversión de applets de Geogebra a HTML5
Dados los problemas que presenta la ejecución de páginas html que contienen applets construidos con Geogebra, describimos en este artículo un procedimiento para construir páginas html que contengan un script de JavaScript generado desde el archivo .ggb de Geogebra, que permiten visualizar escenas creadas con Geogebra, desde cualquier navegador, en equipos conectados a internet. En primer lugar abrimos el archivo .ggb correspondiente a la escena que vamos a convertir. Comprobamos que funciona...Área de conocimientoContexto educativo -
MoviendoFunciones
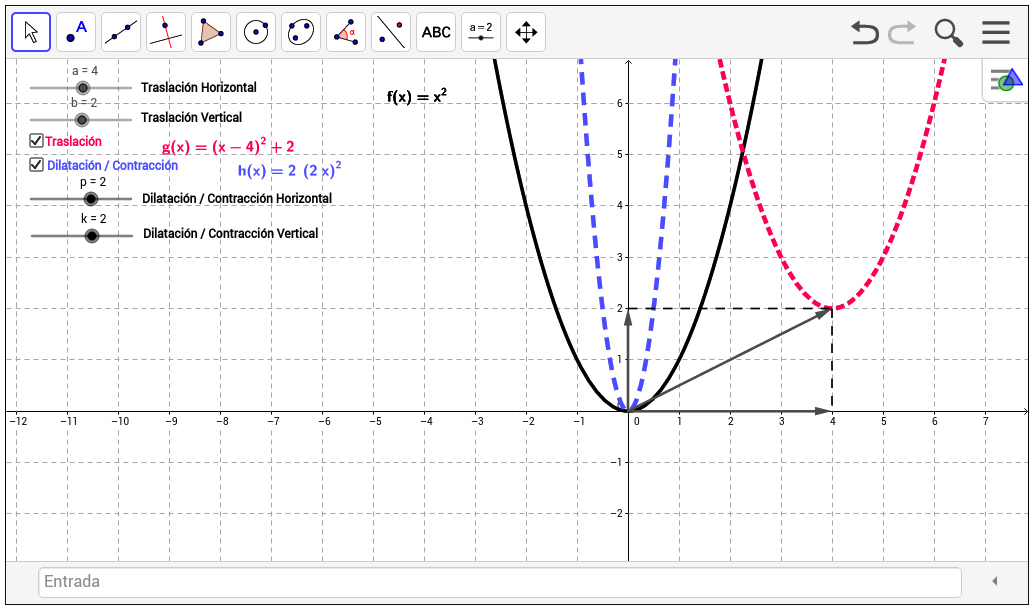 Mi Unidad didáctica integrada sobre Funciones para 1º Bachillerato Matemáticas I: http://procomun.educalab.es/es/ode/view/1445270079507Área de conocimientoContexto educativo
Mi Unidad didáctica integrada sobre Funciones para 1º Bachillerato Matemáticas I: http://procomun.educalab.es/es/ode/view/1445270079507Área de conocimientoContexto educativo -
Applet interactivo: Sistemas de 2 ecuaciones lineales con 2 incógnitas #Geogebra
Applet interactivo: Sistemas de 2 ecuaciones con 2 incógnitas Resolución analítica y gráfica. Clasificación en función del número de soluciones#Geogebrahttp://ow.ly/KCKWvÁrea de conocimientoContexto educativo -
Estudio del límite de una función (en un punto y en el infinito) con #Geogebra #appletinteractivo #html5
Compartoapplet interactivoque he realizado conGeogebrapara trabajar en clase elestudio del límite de una función. http://matematicas11235813.luismiglesias.es/2015/01/25/estudio-del-limite-de-una-funcion-en-un-punto-y-en-el-infinito-con-geogebra-appletinteractivo-html5/Área de conocimientoContexto educativo -
MatemaTicInfantil
 Geogebra para ver las matemáticas con los más pequeños con la PDI. http://catedu.es/MatemaTICinfantil/?p=223 https://twitter.com/jsilva66281071/status/581526296523632641Área de conocimientoContexto educativo
Geogebra para ver las matemáticas con los más pequeños con la PDI. http://catedu.es/MatemaTICinfantil/?p=223 https://twitter.com/jsilva66281071/status/581526296523632641Área de conocimientoContexto educativo -
MatemaTicInfantil
 https://twitter.com/GeoGebreando/status/574169152723795968Área de conocimientoContexto educativo
https://twitter.com/GeoGebreando/status/574169152723795968Área de conocimientoContexto educativo -
GEOMETRÍA EN LA NATURALEZA
 Trabajamos la simetría en la naturaleza. Necesitaremos una cámara fotográfica o en su defecto las cámaras de los móviles. El programa GIMP para manipular la imágenes y el programa geogebra para mostrar insertándolo en las imágenes las transformaciones geométricas correspondientes a las imágenes seleccionadas tanto por red o tomadas en el entorno de nuestro Centro. Lo podeis encontrar en :http://procomun.educalab.es/es/ode/view/1429779838121Área de conocimientoContexto educativo
Trabajamos la simetría en la naturaleza. Necesitaremos una cámara fotográfica o en su defecto las cámaras de los móviles. El programa GIMP para manipular la imágenes y el programa geogebra para mostrar insertándolo en las imágenes las transformaciones geométricas correspondientes a las imágenes seleccionadas tanto por red o tomadas en el entorno de nuestro Centro. Lo podeis encontrar en :http://procomun.educalab.es/es/ode/view/1429779838121Área de conocimientoContexto educativo -
Algunos recursos de matemáticas...para empezar
A continuación comparto con todos los usuarios que hacen posible esta gran red de REA, un par de recursos interesantes relacionados con la enseñanza de las matemáticas. El primero de ellos es el Proyecto Gauss, un portal repleto de recursos realizados con GeoGebra para la enseñanza y el aprendizaje de las matemáticas (http://recursostic.educacion.es/gauss/web/materiales_didacticos/eso/actividades/novedades.htm) En concreto adjunto el enlace a los recursos didácticos para la ESO. Espero que ...Área de conocimientoContexto educativo


