PROCOMÚN
Showing results from 21 to 40 out of 137
-
Progresiones Aritméticas y Geométricas
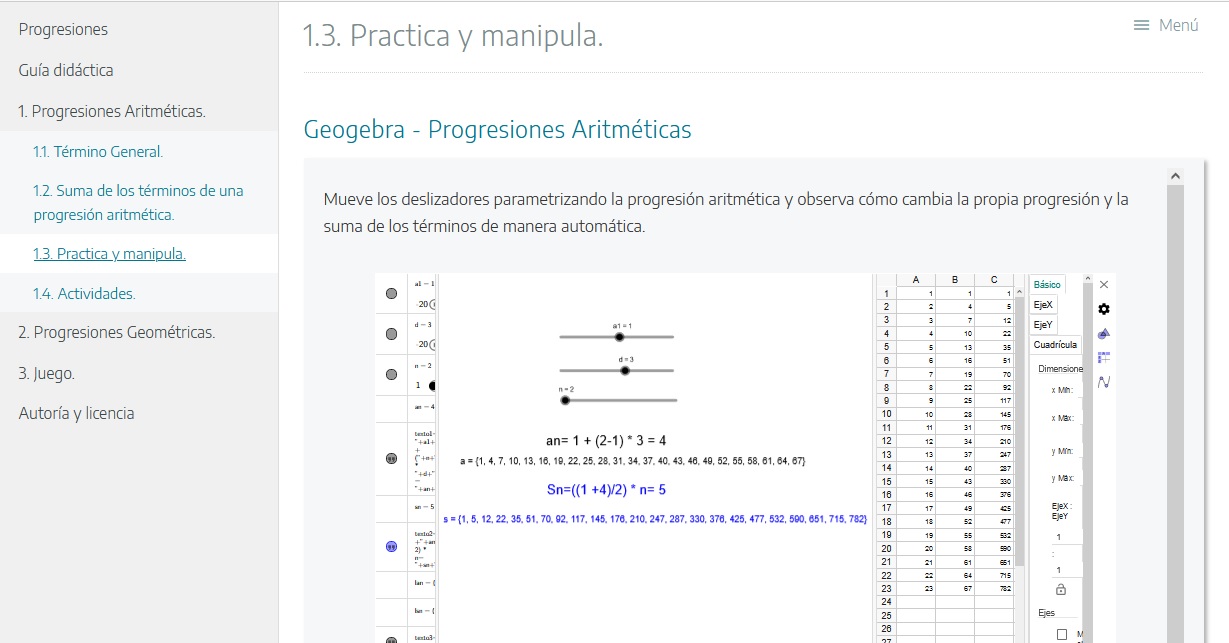 Nivel: 3º E.S.O. Asignatura: Matemáticas Académicas. Bloques de contenido: 1, 3 y 5.Área de conocimientoContexto educativoTipo de recurso
Nivel: 3º E.S.O. Asignatura: Matemáticas Académicas. Bloques de contenido: 1, 3 y 5.Área de conocimientoContexto educativoTipo de recurso -
ARTEMÁTICA
 ABP centrado en el conocimiento y estudio de estilos pictóricos, a través de la digitalización, el arte, las matemáticas y otras disciplinas.Área de conocimientoContexto educativoTipo de recurso
ABP centrado en el conocimiento y estudio de estilos pictóricos, a través de la digitalización, el arte, las matemáticas y otras disciplinas.Área de conocimientoContexto educativoTipo de recurso -
Un paseo por la Alhambra
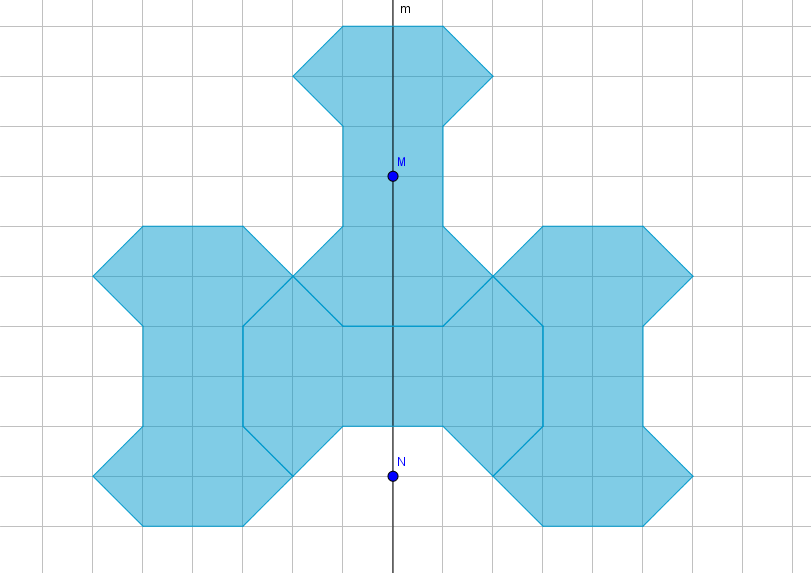 Hola a todos: Estoy muy contenta de poder compartir mi primer Proyecto Flipped Classroom. Estoy muy orgullosa de él porque me ha costado mucho aprender a utilizar todas las herramientas empleadas y sobre todo ponerme las pilas con las TIC. Espero que a alguien le sea útil. Un paseo por la AlhambraÁrea de conocimientoContexto educativo
Hola a todos: Estoy muy contenta de poder compartir mi primer Proyecto Flipped Classroom. Estoy muy orgullosa de él porque me ha costado mucho aprender a utilizar todas las herramientas empleadas y sobre todo ponerme las pilas con las TIC. Espero que a alguien le sea útil. Un paseo por la AlhambraÁrea de conocimientoContexto educativo -
Proyecto Flipped Classroom "Movimientos en el plano"
El proyecto realizado en el curso Flipped Classroom INTEF está dirigido a alumnos de 3º de la ESO, se realiza con una distribución del aula en grupos cooperativos y se necesita conexión a internet y ordenador personal portátil. Os dejo el enlace de la entrada del blog donde se puede encontrar el proyecto detallado (documento word). http://flippedclassroomquim.blogspot.com.es/2017/11/proyecto-final-movimientos-en-el-plano.htmlÁrea de conocimientoContexto educativo -
Web de apoyo a la docencia en Matemáticas
 Web creada con google-sites que sirve para ´poner todo lo relativo a la docencia en Matemáticas, tanto en Secundaria como en Bachillerato. Incluye formularios de hot-potatoes, animaciones Geogebra, google-calendar, repositorio de documentos.....Área de conocimiento
Web creada con google-sites que sirve para ´poner todo lo relativo a la docencia en Matemáticas, tanto en Secundaria como en Bachillerato. Incluye formularios de hot-potatoes, animaciones Geogebra, google-calendar, repositorio de documentos.....Área de conocimiento -
Histograma
 Un histograma está formado por rectángulos adosados (a diferencia de los diagramas de barras, en los que los rectángulos están separados). Las bases de los rectángulos son los intervalos en que se han agrupado los datos. Las alturas respectivas de los rectángulos son las frecuencias de cada uno de dichos intervalos. En esta aplicación vamos a construir el histograma que representa la distribución formada por las alturas, en centímetros, de los 25 alumnos y alumnas de una clase. Se incluye las...Área de conocimientoContexto educativoTipo de recursoCollections
Un histograma está formado por rectángulos adosados (a diferencia de los diagramas de barras, en los que los rectángulos están separados). Las bases de los rectángulos son los intervalos en que se han agrupado los datos. Las alturas respectivas de los rectángulos son las frecuencias de cada uno de dichos intervalos. En esta aplicación vamos a construir el histograma que representa la distribución formada por las alturas, en centímetros, de los 25 alumnos y alumnas de una clase. Se incluye las...Área de conocimientoContexto educativoTipo de recursoCollections -
Composición de isometrías
 Escena en geogebra para ver cómo se componen las isometrías y tratar de encontrar una isometría equivalente a la composición de dos isometrías cualesquiera.Área de conocimientoContexto educativoTipo de recursoCollections
Escena en geogebra para ver cómo se componen las isometrías y tratar de encontrar una isometría equivalente a la composición de dos isometrías cualesquiera.Área de conocimientoContexto educativoTipo de recursoCollections -
Teorema de Pitágoras (demostración de Leonardo da Vinci)
 Se analiza la demostración del teorema de Pitágoras realizada por Leonardo da Vinci.Área de conocimientoContexto educativoTipo de recursoCollections
Se analiza la demostración del teorema de Pitágoras realizada por Leonardo da Vinci.Área de conocimientoContexto educativoTipo de recursoCollections -
Prismas y antiprismas
 Un prisma es un poliedro limitado por dos polígonos iguales y paralelos, llamados bases, y por caras laterales que son paralelogramos que unen los correspondientes lados de las bases. Si las caras laterales son rectangulares, el prisma se llama prisma recto y en caso contrario se llama prisma oblicuo. En el caso del antiprisma las caras laterales son triángulos. Aquí nos limitaremos a ver prismas y antiprismas con bases regulares. Incluye las soluciones a las actividades propuestas.Área de conocimientoContexto educativoTipo de recursoCollections
Un prisma es un poliedro limitado por dos polígonos iguales y paralelos, llamados bases, y por caras laterales que son paralelogramos que unen los correspondientes lados de las bases. Si las caras laterales son rectangulares, el prisma se llama prisma recto y en caso contrario se llama prisma oblicuo. En el caso del antiprisma las caras laterales son triángulos. Aquí nos limitaremos a ver prismas y antiprismas con bases regulares. Incluye las soluciones a las actividades propuestas.Área de conocimientoContexto educativoTipo de recursoCollections -
Medir sobre el histograma
 El histograma es uno de los gráficos estadísticos que manejamos más habitualmente. A partir del histograma podemos hacernos una idea bastante aproximada de la media aritmética y de la desviación típica de la distribución que se representa, que son, como sabes, dos de los parámetros que utilizamos para resumir un conjunto de datos. En esta aplicación debes encontrar los valores de la media aritmética y de la desviación típica de los histogramas que se presentan. Las actividades propuestas incl...Área de conocimientoContexto educativoTipo de recursoCollections
El histograma es uno de los gráficos estadísticos que manejamos más habitualmente. A partir del histograma podemos hacernos una idea bastante aproximada de la media aritmética y de la desviación típica de la distribución que se representa, que son, como sabes, dos de los parámetros que utilizamos para resumir un conjunto de datos. En esta aplicación debes encontrar los valores de la media aritmética y de la desviación típica de los histogramas que se presentan. Las actividades propuestas incl...Área de conocimientoContexto educativoTipo de recursoCollections -
Teorema de Pitágoras (demostración de Pappus)
 Se analiza la demostración del teorema de Pitágoras realizada por Pappus de Alejandría, un importante matemático del siglo III.Área de conocimientoContexto educativoTipo de recursoCollections
Se analiza la demostración del teorema de Pitágoras realizada por Pappus de Alejandría, un importante matemático del siglo III.Área de conocimientoContexto educativoTipo de recursoCollections -
Distancia al horizonte
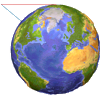 Se practica con el teorema de Pitágoras para averiguar a qué distancia se ve el horizonte desde el borde del mar a partir de la altura fr los ojos y el radio aproximado de la Tierra.Área de conocimientoContexto educativoTipo de recursoCollections
Se practica con el teorema de Pitágoras para averiguar a qué distancia se ve el horizonte desde el borde del mar a partir de la altura fr los ojos y el radio aproximado de la Tierra.Área de conocimientoContexto educativoTipo de recursoCollections -
Corona
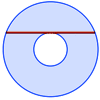 Utilizando Geogebra, se realiza una construcción para relacionar el teorema de Pitágoras con el área de una corona circular.Área de conocimientoContexto educativoTipo de recursoCollections
Utilizando Geogebra, se realiza una construcción para relacionar el teorema de Pitágoras con el área de una corona circular.Área de conocimientoContexto educativoTipo de recursoCollections -
Sombrilla
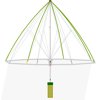 La apertura y cierre de un paraguas o una sombrilla se rige por un sencillo mecanismo. En esta actividad se explora en qué propiedades geométricas se basa ese mecanismo.Área de conocimientoContexto educativoTipo de recursoCollections
La apertura y cierre de un paraguas o una sombrilla se rige por un sencillo mecanismo. En esta actividad se explora en qué propiedades geométricas se basa ese mecanismo.Área de conocimientoContexto educativoTipo de recursoCollections -
Simetría axial (autoevaluación)
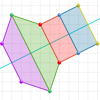 Cuando un figura tiene simetría axial, a cada punto a un lado del eje le corresponde otro punto (que se llama "punto reflejado" o "imagen") al otro lado del eje y a la misma distancia del eje, de forma que la línea que los une es perpendicular al eje. En esta actividad hay que crear figuras que tengan simetría axial, a partir del eje de simetría que la aplicación muestra. Se puede elegir el número de puntos que hay que reflejar en el eje, así como el nivel de dificultad.Área de conocimientoContexto educativoTipo de recursoCollections
Cuando un figura tiene simetría axial, a cada punto a un lado del eje le corresponde otro punto (que se llama "punto reflejado" o "imagen") al otro lado del eje y a la misma distancia del eje, de forma que la línea que los une es perpendicular al eje. En esta actividad hay que crear figuras que tengan simetría axial, a partir del eje de simetría que la aplicación muestra. Se puede elegir el número de puntos que hay que reflejar en el eje, así como el nivel de dificultad.Área de conocimientoContexto educativoTipo de recursoCollections -
Simetría axial
 En esta actividad se pueden dibujar figuras que tengan simetría axial, a partir del eje de simetría que la aplicación muestra.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad se pueden dibujar figuras que tengan simetría axial, a partir del eje de simetría que la aplicación muestra.Área de conocimientoContexto educativoTipo de recursoCollections -
Píllame
 En esta actividad se presenta un juego para dos jugadores. Cada uno con una ficha trata de pillar al otro.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad se presenta un juego para dos jugadores. Cada uno con una ficha trata de pillar al otro.Área de conocimientoContexto educativoTipo de recursoCollections -
Billar circular
 En un billar normal, la bola rebota en la banda de forma simétrica respecto a la perpendicular a la banda en el punto de contacto, formando ángulos iguales a ambos lados. En esta actividad, en cambio, se practica el juego del billar con una banda curva, en ese caso el eje de simetría es la perpendicular a la recta tangente a la curva en ese punto. En el caso de un billar circular, esa perpendicular es siempre el radio del círculo.Área de conocimientoContexto educativoTipo de recursoCollections
En un billar normal, la bola rebota en la banda de forma simétrica respecto a la perpendicular a la banda en el punto de contacto, formando ángulos iguales a ambos lados. En esta actividad, en cambio, se practica el juego del billar con una banda curva, en ese caso el eje de simetría es la perpendicular a la recta tangente a la curva en ese punto. En el caso de un billar circular, esa perpendicular es siempre el radio del círculo.Área de conocimientoContexto educativoTipo de recursoCollections -
Cualquier triángulo tesela
 Se comprueba mediante una sencilla construcción Geogebra que cualquier azulejo triangular puede teselar el plano.Área de conocimientoContexto educativoTipo de recursoCollections
Se comprueba mediante una sencilla construcción Geogebra que cualquier azulejo triangular puede teselar el plano.Área de conocimientoContexto educativoTipo de recursoCollections -
Mosaicos regulares y semirregulares
 En otras actividades se comprueba que los únicos polígonos regulares que teselan el plano son: Triángulos equiláteros, cuadrados y hexágonos regulares. En esta actividad se hacen prácticas con teselados o mosaicos que se denominan semirregulares y que se forman combinando dos o más tipos de polígonos regulares, distribuidos de tal modo que en todos los vértices aparecen los mismos polígonos y colocados en el mismo orden.Área de conocimientoContexto educativoTipo de recursoCollections
En otras actividades se comprueba que los únicos polígonos regulares que teselan el plano son: Triángulos equiláteros, cuadrados y hexágonos regulares. En esta actividad se hacen prácticas con teselados o mosaicos que se denominan semirregulares y que se forman combinando dos o más tipos de polígonos regulares, distribuidos de tal modo que en todos los vértices aparecen los mismos polígonos y colocados en el mismo orden.Área de conocimientoContexto educativoTipo de recursoCollections


