PROCOMÚN
Showing results from 21 to 40 out of 120
-
Píllame
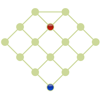 En esta actividad se presenta un juego para dos jugadores. Cada uno con una ficha trata de pillar al otro.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad se presenta un juego para dos jugadores. Cada uno con una ficha trata de pillar al otro.Área de conocimientoContexto educativoTipo de recursoCollections -
Billar circular
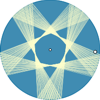 En un billar normal, la bola rebota en la banda de forma simétrica respecto a la perpendicular a la banda en el punto de contacto, formando ángulos iguales a ambos lados. En esta actividad, en cambio, se practica el juego del billar con una banda curva, en ese caso el eje de simetría es la perpendicular a la recta tangente a la curva en ese punto. En el caso de un billar circular, esa perpendicular es siempre el radio del círculo.Área de conocimientoContexto educativoTipo de recursoCollections
En un billar normal, la bola rebota en la banda de forma simétrica respecto a la perpendicular a la banda en el punto de contacto, formando ángulos iguales a ambos lados. En esta actividad, en cambio, se practica el juego del billar con una banda curva, en ese caso el eje de simetría es la perpendicular a la recta tangente a la curva en ese punto. En el caso de un billar circular, esa perpendicular es siempre el radio del círculo.Área de conocimientoContexto educativoTipo de recursoCollections -
Cualquier triángulo tesela
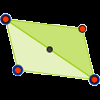 Se comprueba mediante una sencilla construcción Geogebra que cualquier azulejo triangular puede teselar el plano.Área de conocimientoContexto educativoTipo de recursoCollections
Se comprueba mediante una sencilla construcción Geogebra que cualquier azulejo triangular puede teselar el plano.Área de conocimientoContexto educativoTipo de recursoCollections -
Mosaicos regulares y semirregulares
 En otras actividades se comprueba que los únicos polígonos regulares que teselan el plano son: Triángulos equiláteros, cuadrados y hexágonos regulares. En esta actividad se hacen prácticas con teselados o mosaicos que se denominan semirregulares y que se forman combinando dos o más tipos de polígonos regulares, distribuidos de tal modo que en todos los vértices aparecen los mismos polígonos y colocados en el mismo orden.Área de conocimientoContexto educativoTipo de recursoCollections
En otras actividades se comprueba que los únicos polígonos regulares que teselan el plano son: Triángulos equiláteros, cuadrados y hexágonos regulares. En esta actividad se hacen prácticas con teselados o mosaicos que se denominan semirregulares y que se forman combinando dos o más tipos de polígonos regulares, distribuidos de tal modo que en todos los vértices aparecen los mismos polígonos y colocados en el mismo orden.Área de conocimientoContexto educativoTipo de recursoCollections -
Quita y pon curvas de Bézier
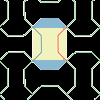 Se explican las curvas de Bézier cuadráticas. Al iniciarse, la siguiente aplicación muestra un azulejo con forma de hueso. Se trata de un famoso motivo que aparece en la Alhambra, conocido como "el hueso nazarí". Con ayuda de esas curvas, podemos modificar fácilmente la forma de un azulejo, de tal modo que, una vez modificado, el azulejo siga teselando. Este método se conoce como "quita y pon", porque básicamente consiste en poner en un lado lo que se ha quitado del otro.Área de conocimientoContexto educativoTipo de recursoCollections
Se explican las curvas de Bézier cuadráticas. Al iniciarse, la siguiente aplicación muestra un azulejo con forma de hueso. Se trata de un famoso motivo que aparece en la Alhambra, conocido como "el hueso nazarí". Con ayuda de esas curvas, podemos modificar fácilmente la forma de un azulejo, de tal modo que, una vez modificado, el azulejo siga teselando. Este método se conoce como "quita y pon", porque básicamente consiste en poner en un lado lo que se ha quitado del otro.Área de conocimientoContexto educativoTipo de recursoCollections -
Mosaicos pivotantes
 En esta actividad se pueden ver tres ejemplos de mosaicos pivotantes. Si imaginamos que los polígonos que forman parte de un mosaico son piezas sólidas engarzadas entre sí en sus vértices mediante pivotes (ejes o bisagras) que les permiten girar entonces, en algunos casos, al hacer girar las piezas se abren espacios huecos entre ellas que crean nuevos mosaicos.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad se pueden ver tres ejemplos de mosaicos pivotantes. Si imaginamos que los polígonos que forman parte de un mosaico son piezas sólidas engarzadas entre sí en sus vértices mediante pivotes (ejes o bisagras) que les permiten girar entonces, en algunos casos, al hacer girar las piezas se abren espacios huecos entre ellas que crean nuevos mosaicos.Área de conocimientoContexto educativoTipo de recursoCollections -
Los 14 pentágonos convexos que teselan
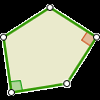 En esta actividad se puede ver que aunque los pentágonos regulares no pueden teselar el plano, existen al menos 14 familias de pentágonos convexos irregulares que logran teselarlo.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad se puede ver que aunque los pentágonos regulares no pueden teselar el plano, existen al menos 14 familias de pentágonos convexos irregulares que logran teselarlo.Área de conocimientoContexto educativoTipo de recursoCollections -
Los 3 hexágonos convexos que teselan
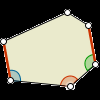 En esta actividad se puede ver que los hexágonos regulares pueden teselar el plano. Por otra parte, la clasificación de polígonos cóncavos que teselen es un problema demasiado amplio para ser abordado, salvo casos particulares (como los poliominós y los poliamantes) a los que se puede acceder también desde esta actividad aunque existe una específica dedicada a ellos.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad se puede ver que los hexágonos regulares pueden teselar el plano. Por otra parte, la clasificación de polígonos cóncavos que teselen es un problema demasiado amplio para ser abordado, salvo casos particulares (como los poliominós y los poliamantes) a los que se puede acceder también desde esta actividad aunque existe una específica dedicada a ellos.Área de conocimientoContexto educativoTipo de recursoCollections -
Carretillas de Penrose
 La carretilla de Penrose es un poliamante de orden 18 (un poliamante es un polígono formado por triángulos equiláteros iguales unidos entre sí por sus lados). La clave para rellenar el plano con esta tesela consiste en formar con 12 de ellas un polígono base con el que, finalmente, se podrá rellenar el plano mediante sucesivas traslaciones. En esta aplicación se trata de completar ese polígono base.Área de conocimientoContexto educativoTipo de recursoCollections
La carretilla de Penrose es un poliamante de orden 18 (un poliamante es un polígono formado por triángulos equiláteros iguales unidos entre sí por sus lados). La clave para rellenar el plano con esta tesela consiste en formar con 12 de ellas un polígono base con el que, finalmente, se podrá rellenar el plano mediante sucesivas traslaciones. En esta aplicación se trata de completar ese polígono base.Área de conocimientoContexto educativoTipo de recursoCollections -
Cualquier cuadrilátero tesela
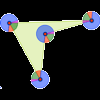 Se comprueba mediante una sencilla construcción Geogebra que cualquier azulejo en forma de cuadrilátero puede teselar el plano.Área de conocimientoContexto educativoTipo de recursoCollections
Se comprueba mediante una sencilla construcción Geogebra que cualquier azulejo en forma de cuadrilátero puede teselar el plano.Área de conocimientoContexto educativoTipo de recursoCollections -
Dardos y cometas
 En esta actividad se pueden construir atractivos (y difíciles) mosaicos con las dos teselas Dardo y Cometa. Con infinitas copias de una tesela, o de una colección de teselas distintas, se pueden realizar mosaicos aperiódicos, es decir, mosaicos donde ningún movimiento de traslación hará que una copia coincida con el original.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad se pueden construir atractivos (y difíciles) mosaicos con las dos teselas Dardo y Cometa. Con infinitas copias de una tesela, o de una colección de teselas distintas, se pueden realizar mosaicos aperiódicos, es decir, mosaicos donde ningún movimiento de traslación hará que una copia coincida con el original.Área de conocimientoContexto educativoTipo de recursoCollections -
Mosaicos aperiódicos
 Mediante una sencilla construcción en Geogebra se contruyen mosaicos aperiódicos con dos tipos de azulejos: Pentágono equilátero cóncavo y Pentágono regular, estrella de cinco puntas, decágono regular y "ocho". Se observa con la cosntrucción que con copias de un mismo azulejo podemos realizar mosaicos aperiódicos, es decir, mosaicos donde ningún movimiento de traslación hará que una copia coincida con el original. En ambos casos, con los mismos azulejos también se pueden crear mosaicos perió...Área de conocimientoContexto educativoTipo de recursoCollections
Mediante una sencilla construcción en Geogebra se contruyen mosaicos aperiódicos con dos tipos de azulejos: Pentágono equilátero cóncavo y Pentágono regular, estrella de cinco puntas, decágono regular y "ocho". Se observa con la cosntrucción que con copias de un mismo azulejo podemos realizar mosaicos aperiódicos, es decir, mosaicos donde ningún movimiento de traslación hará que una copia coincida con el original. En ambos casos, con los mismos azulejos también se pueden crear mosaicos perió...Área de conocimientoContexto educativoTipo de recursoCollections -
Creador de rosetones
 En esta actividad se puede crear un diseño propio de un rosetón. Para ello primero hay que elegir, con ayuda de los deslizadores, el grupo de isometrías, es decir, los tipos de simetrías que queremos que aparezcan.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad se puede crear un diseño propio de un rosetón. Para ello primero hay que elegir, con ayuda de los deslizadores, el grupo de isometrías, es decir, los tipos de simetrías que queremos que aparezcan.Área de conocimientoContexto educativoTipo de recursoCollections -
Grupos Diedros (*n,nm)
 Una vez leída la información sobre el Grupo de isometrías de los rosetones, a la que se puede acceder desde la misma página, en la escena se explora la clase de losDiedros (*n, nm), la segunda de las dos clases de rosetones, realizando las construcciones indicadas o mediante diseños libres de azulejos. Es recomendable realizar antes de esta la actividad sobre la otra clase de rosetones, la de los rosetones Cíclicos.Área de conocimientoContexto educativoTipo de recursoCollections
Una vez leída la información sobre el Grupo de isometrías de los rosetones, a la que se puede acceder desde la misma página, en la escena se explora la clase de losDiedros (*n, nm), la segunda de las dos clases de rosetones, realizando las construcciones indicadas o mediante diseños libres de azulejos. Es recomendable realizar antes de esta la actividad sobre la otra clase de rosetones, la de los rosetones Cíclicos.Área de conocimientoContexto educativoTipo de recursoCollections -
Grupo cíclico (n,n)
 Una vez leída la información sobre el Grupo de isometrías de los rosetones, a la que se puede acceder desde la misma página, en la escena se explora la clase de los Cíclicos (n, n), la primera de las dos clases de rosetones, realizando las construcciones indicadas o mediante diseños libres de azulejos.Área de conocimientoContexto educativoTipo de recursoCollections
Una vez leída la información sobre el Grupo de isometrías de los rosetones, a la que se puede acceder desde la misma página, en la escena se explora la clase de los Cíclicos (n, n), la primera de las dos clases de rosetones, realizando las construcciones indicadas o mediante diseños libres de azulejos.Área de conocimientoContexto educativoTipo de recursoCollections -
Problemas de exploración de mosaicos
 Esta actividad te permitirá demostrar tu habilidad para encontrar el grupo de isometrías correspondiente a un mosaico. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Es aconsejable realizar primero las actividades planteadas en la aplicación de esta misma colección llamada "Prácticas de exploración de mosaicos". Se incluyen las soluciones de las actividades propuestas.Área de conocimientoContexto educativoTipo de recursoCollections
Esta actividad te permitirá demostrar tu habilidad para encontrar el grupo de isometrías correspondiente a un mosaico. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Es aconsejable realizar primero las actividades planteadas en la aplicación de esta misma colección llamada "Prácticas de exploración de mosaicos". Se incluyen las soluciones de las actividades propuestas.Área de conocimientoContexto educativoTipo de recursoCollections -
Creador de mosaicos
 Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. En esta actividad se puede crear un diseño propio de un mosaico. Para ello primero hay que elegir el grupo de isometrías, situar los vértices del azulejo que se repite por traslación y dibujar el motivo decorativo en la región sombreada.Área de conocimientoContexto educativoTipo de recursoCollections
Antes de empezar con los frisos se debe leer la información general sobre los grupos de isometrías de los mosaicos periódicos a la que se puede acceder desde la misma página. En esta actividad se puede crear un diseño propio de un mosaico. Para ello primero hay que elegir el grupo de isometrías, situar los vértices del azulejo que se repite por traslación y dibujar el motivo decorativo en la región sombreada.Área de conocimientoContexto educativoTipo de recursoCollections -
Prácticas de exploración de mosaicos
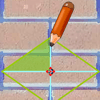 Esta actividad te permitirá practicar el procedimiento para averiguar a qué grupo de isometrías corresponde un mosaico cualquiera. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Las actividades propuestas se comprueban con su propia autoevaluación.Área de conocimientoContexto educativoTipo de recursoCollections
Esta actividad te permitirá practicar el procedimiento para averiguar a qué grupo de isometrías corresponde un mosaico cualquiera. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Las actividades propuestas se comprueban con su propia autoevaluación.Área de conocimientoContexto educativoTipo de recursoCollections -
Explorador de mosaicos
 Esta actividad te permitirá explorar un mosaico periódico cualquiera y averiguar a qué grupo de isometrías corresponde. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Es aconsejable realizar primero las actividades planteadas en la aplicación de esta misma colección llamada "Prácticas de exploración de mosaicos". Las actividades propuestas se comprueban con su propia autoevaluación.Área de conocimientoContexto educativoTipo de recursoCollections
Esta actividad te permitirá explorar un mosaico periódico cualquiera y averiguar a qué grupo de isometrías corresponde. Recuerda que aquí no hacemos distinción por color, solo nos fijamos en las formas, es decir, en el contorno y diseño del motivo decorativo. Es aconsejable realizar primero las actividades planteadas en la aplicación de esta misma colección llamada "Prácticas de exploración de mosaicos". Las actividades propuestas se comprueban con su propia autoevaluación.Área de conocimientoContexto educativoTipo de recursoCollections -
Mosaicos periódicos, grupo 17
 En esta actividad explorarás el último grupo de isometrías, el grupo 17 (*632, p6m). Es el último de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de diamante. Se incluye las soluciones de las actividades propuestas.Área de conocimientoContexto educativoTipo de recursoCollections
En esta actividad explorarás el último grupo de isometrías, el grupo 17 (*632, p6m). Es el último de los cinco grupos de mosaicos que se pueden crear con azulejos con forma de diamante. Se incluye las soluciones de las actividades propuestas.Área de conocimientoContexto educativoTipo de recursoCollections


