Se visualiza la concoide de rosetón, también llamada pétalo geométrico. Se trata de una familia de curvas que parece haber nacido para identificarse con algunas de las flores más habituales en el campo o en las floristerías. En esta aplicación vamos a conocer un poco mejor sus características, investigando cómo cambia su forma en función de los parámetros que la determinan.

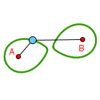Aparecen varias curvas diferentes (Circunferencia, Elipse, Hipérbola, Parábola y Óvalo de Cassini) y hay que identificar cuáles son las propiedades invariantes que conservan cada una de las curvas que se presentan.

Aparece una escena en Geogebra con tres apartados en cada uno de los cuales se muestra una espiral diferente: Invlouta de un círculo, espiral de Arquímedes y espiral logarítmica. Se pueden modificar los parámetros para ver como afectan en la forma de cada una de las espirales. Finalmente se pueden mostrar imágenes tomadas de la realidad y comprobar que su forma se ajusta a alguna de las espirales estudiadas (caracoles, figuras escultóricas, un ciclón, la galaxia...)

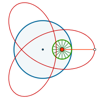Explorar varias familias de curvas que pueden generarse mediante el movimiento de una circunferencia que gira alrededor de otra, por fuera o por dentro. Son las epitrocoides e hipotrocoides.

Utilizando algunas herramientas de Geogebra para medir longitudes y áreas en la escena se practica el concepto de plano y escala.

Utilizando algunas herramientas de Geogebra se trata de medir áreas de figuras, como un trozo de cartulina en forma de polígono irregular, averiguando primero la escala mediante la razón entre la medida en el plano de una moneda y su medida real.

Para comprender la utilidad de las escalas logarítmicas podemos ver en esta actividad que se usan en diversas áreas y situaciones. Un caso muy conocido es la escala Richter que utilizamos para clasificar los seísmos. Si utilizamos en un eje de coordenadas una escala logarítmica y en el otro eje una escala aritmética se dice que estamos en presencia de un sistema de referencia semilogarítmico. Si en ambos ejes utilizamos escalas logarítmicas, el sistema de referencia es logarítmico.

Vamos a ver cómo podemos aprovechar la probabilidad para aproximar el resultado de cálculos complicados sin necesidad de hacerlos. Esta aplicación simula una diana sobre la que se figuran disparos, se asocia probabilidad con los resultados de los disparos. Se incluye las soluciones de las actividades propuestas.

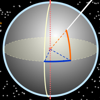Primera aplicación de un conjunto sobre la Tierra, en esta actividad se estudias conceptos relacionados con los mapas y la imposibilidad de una representación perfecta sobre el plano. Se incluye las soluciones de las actividades propuestas.

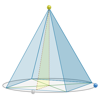Una pirámide es un poliedro limitado por una base poligonal y por caras laterales triangulares que coinciden en un punto llamado ápice. Si todas las caras laterales son iguales, la pirámide se llama pirámide recta y en caso contrario se llama pirámide oblicua. En esta aplicación nos limitaremos a ver pirámides con base regular. Incluye las soluciones a las actividades propuestas.

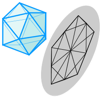Para facilitar el estudio de diversos aspectos de los cuerpos espaciales los matemáticos descubrieron que una buena estrategia consiste en observar su proyección sobre el plano, es decir, su sombra. Al proyectar un poliedro, los Vértices (blancos) se proyectan en Nodos (de color naranja), las Aristas pasan a ser Líneas rectas que unen los Nodos, y las Caras del poliedro pasan a ser Regiones poligonales (con vértices en los Nodos). La gran ventaja de esta transformación es que nos resulta much...

En esta actividad se estudia uno de los casos de dualidad entre poliedros regulares. Las caras de uno de los poliedros, en este caso del tetraedro, se corresponde con cada uno de los vértices del otro, que en este caso es también un tetraedro y. a su vez, cada una de las caras del segundo, tetraedro, se corresponde con cada uno de los vértices del primero. Esta correspondencia se denomina dualidad. En la escena Geogebra se puede observar como, mediante truncamiento, uno se convierte en el otr...

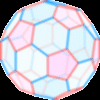En esta actividad se estudia uno de los casos de dualidad entre poliedros regulares. Las caras de uno de los poliedros, en este caso del icosaedro, se corresponde con cada uno de los vértices del otro, aqui el dodecaedro y. a su vez, cada una de las caras del dodecaedro se corresponde con cada uno de los vértices del icosaedro. Esta correspondencia se denomina dualidad. En la escena Geogebra se puede observar como, mediante truncamiento, uno se convierte en el otro. En este proceso aparecen o...

La forma habitual de realizar un recuento es anotando una marca cada vez que contamos una unidad más. Dicha notación se complica a medida que se aumenta el número. En esta aplicación se realiza un estudio sobre agrupaciones y conteo. Las actividades que interviene incluye su autoevaluación.

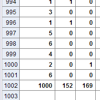Las bases de datos y hojas de cálculo son herramientas muy poderosas, actualmente imprescindibles, para realizar rápidamente cálculos que afectan a grandes cantidades de datos. GeoGebra incorpora una hoja de cálculo. Vamos a aprovecharla para practicar los procedimientos habituales en esas tablas dinámicas llamadas "hojas de cálculo", como son introducir datos, copiar cálculos de forma masiva y realizar rápidas operaciones con gran número de valores. Las actividades que se proponen incluyen s...

Aplicación que con el fondo del cuento de Edgar Allan Poe de mismo nombre, donde el protagonista (el señor Legrand) encuentra un tesoro gracias a que es capaz de descifrar un texto en clave con las pistas suficientes para ir en su busca. Con este telón de fondo se plantean diversas cuestiones. Se incluye las soluciones de las actividades propuestas.

La esperanza de vida es un dato que valora la salud de la población, mientras que la renta per cápita valora su bienestar económico. Estudio estadístico basado en estos dos datos a través del tiempo, permite reflexionar sobre el nivel de vida utilizando una herramienta matemática. Se incluye las soluciones de las actividades propuestas.

A partir de la observación de la representación mediante una construcción en Geogebra del mecanismo que hace funcionar una caja de música, se trata de observar el comportamiento de las funciones periódicas.

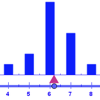La forma del diagrama de barras o del histograma nos permite calcular "a ojo", con bastante aproximación, el valor de la media aritmética de los datos representados. La media aritmética coincide con el "punto de equilibrio" del gráfico o, dicho de otro modo, con la proyección sobre el eje horizontal de su centro de gravedad. Se incluye las soluciones de las actividades propuestas.

La media aritmética y la desviación típica son los parámetros más utilizados para resumir una colección de datos. La media es el valor que resulta de compensar unos datos con otros, para conseguir que todos los datos sean iguales. En esta aplicación trataremos de encontrar la relación entre los valores de la media aritmética y de la desviación típica de una distribución y la forma del histograma que la representa. Se incluye las soluciones de las actividades propuestas.