PROCOMÚN
Es mostren els resultats 61 a 80 d'un total de 255
-
dominio.zip
 La situación de aprendizaje-actividad está temporalizada dentro de la unidad de Funciones elementales, donde uno de los apartados más importantes es la determinación de l dominio de una función. En el aula se trabaja previamente la determinación del dominio de una furnción de forma analítica. La actividad para realizar en casa consistirá en Determinar el dominio de diferentes funciones (visto su estudio analítico en el aula). En la actividad el alumnado tendrá que determinar analíticamente e...Àrea de coneixementContext educatiuTipus de recurs
La situación de aprendizaje-actividad está temporalizada dentro de la unidad de Funciones elementales, donde uno de los apartados más importantes es la determinación de l dominio de una función. En el aula se trabaja previamente la determinación del dominio de una furnción de forma analítica. La actividad para realizar en casa consistirá en Determinar el dominio de diferentes funciones (visto su estudio analítico en el aula). En la actividad el alumnado tendrá que determinar analíticamente e...Àrea de coneixementContext educatiuTipus de recurs -
FUNCIONES Y GEOGEBRA
 REPRESENTACIÓN DE FUNCIONES CON GEOGEBRA PARA 4º DE ESOÀrea de coneixementContext educatiuTipus de recurs
REPRESENTACIÓN DE FUNCIONES CON GEOGEBRA PARA 4º DE ESOÀrea de coneixementContext educatiuTipus de recurs -
Funcions en Geogebra-Cristina Bonafé Martín.pdf
 Els estudinats utilitzaran Geogebra per a construir una funció definida a trossos, visualitzant com diferents expressions matemàtiques es combinen en una sola gràfica.Àrea de coneixementContext educatiuTipus de recurs
Els estudinats utilitzaran Geogebra per a construir una funció definida a trossos, visualitzant com diferents expressions matemàtiques es combinen en una sola gràfica.Àrea de coneixementContext educatiuTipus de recurs -
FUNCIONES EN LA VIDA COTIDIANA 4º ESOA
 El alumnado debe investigar acerca de diferentes funciones y encontrar aquelllas que representen un fenómeno de la naturaleza. Esta propuesta permite aplicar el concepto de funciones para investigar y modelar el movimiento, lo que proporciona una experiencia significativa y práctica en el estudio de funciones.Àrea de coneixementContext educatiuTipus de recurs
El alumnado debe investigar acerca de diferentes funciones y encontrar aquelllas que representen un fenómeno de la naturaleza. Esta propuesta permite aplicar el concepto de funciones para investigar y modelar el movimiento, lo que proporciona una experiencia significativa y práctica en el estudio de funciones.Àrea de coneixementContext educatiuTipus de recurs -
Explorando parábolas
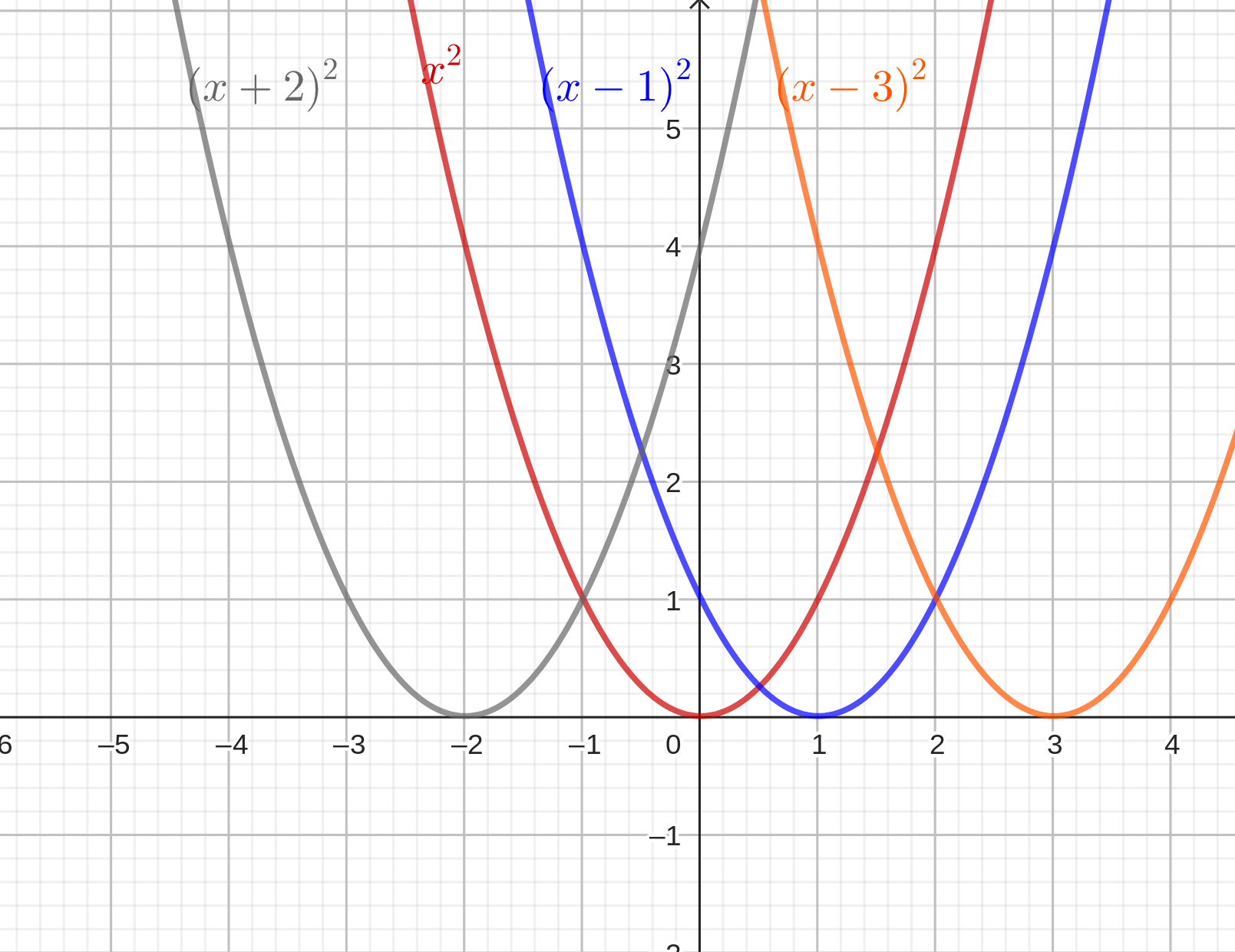 Este REA va dirigido a un nivel de 4ºESO, en clase de matemáticas B, trabajaremos con funciones cuadráticas y su representación (parábolas), y culmina en la creación de un escape room con GeniallyÀrea de coneixementContext educatiuTipus de recurs
Este REA va dirigido a un nivel de 4ºESO, en clase de matemáticas B, trabajaremos con funciones cuadráticas y su representación (parábolas), y culmina en la creación de un escape room con GeniallyÀrea de coneixementContext educatiuTipus de recurs -
Explorando las funciones lineales con GeoGebra
 Este recurso educativo interactivo está diseñado para ayudar a los estudiantes a comprender y aplicar conceptos fundamentales sobre funciones lineales utilizando GeoGebra. A través de explicaciones teóricas, ejercicios prácticos y simulaciones interactivas, los alumnos podrán visualizar la representación gráfica de las funciones lineales, analizar la pendiente y la ordenada en el origen, y experimentar con distintos valores para observar cambios en la gráfica. El material incluye: ✅ Tutor...Àrea de coneixementContext educatiuTipus de recurs
Este recurso educativo interactivo está diseñado para ayudar a los estudiantes a comprender y aplicar conceptos fundamentales sobre funciones lineales utilizando GeoGebra. A través de explicaciones teóricas, ejercicios prácticos y simulaciones interactivas, los alumnos podrán visualizar la representación gráfica de las funciones lineales, analizar la pendiente y la ordenada en el origen, y experimentar con distintos valores para observar cambios en la gráfica. El material incluye: ✅ Tutor...Àrea de coneixementContext educatiuTipus de recurs -
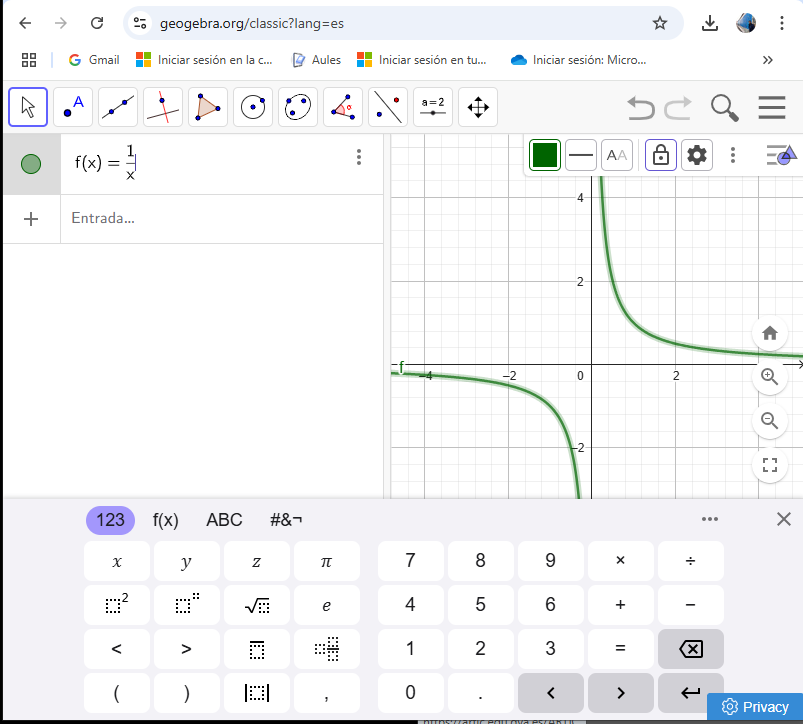
Geometría básica con Geogebra
 GeoGebra es un software matemático interactivo que combina elementos de geometría, álgebra, cálculo y estadística. Fue desarrollado para ayudar a los estudiantes y profesores a visualizar y explorar conceptos matemáticos de manera dinámica. Con el manual siguiente los alumnos comenzarán a trabajar elementos básicos de la geometría mediante Geogebra, además aprenderán los comando elementales de dicho recurso. Enlace al recurso GeoGebra: https://www.geogebra.org/classic?lang=esÀrea de coneixementContext educatiuTipus de recurs
GeoGebra es un software matemático interactivo que combina elementos de geometría, álgebra, cálculo y estadística. Fue desarrollado para ayudar a los estudiantes y profesores a visualizar y explorar conceptos matemáticos de manera dinámica. Con el manual siguiente los alumnos comenzarán a trabajar elementos básicos de la geometría mediante Geogebra, además aprenderán los comando elementales de dicho recurso. Enlace al recurso GeoGebra: https://www.geogebra.org/classic?lang=esÀrea de coneixementContext educatiuTipus de recurs -
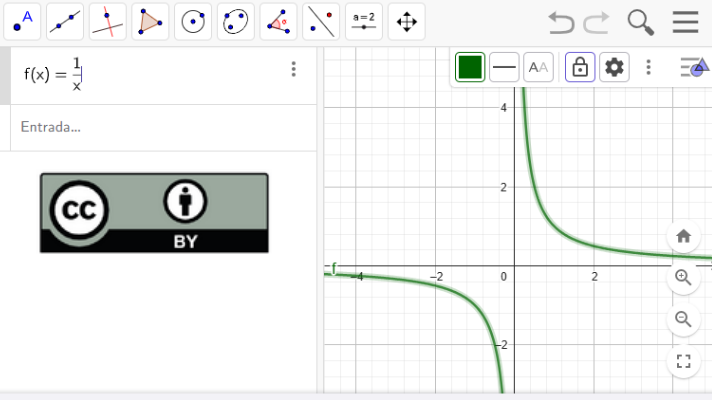
Determinando el dominio de una función
 Licencia CC by Creative Commons El dominio de una función f(x) viene determinado por aquellos valores que puedo tomar la x para que exista la función. Si todavía no tienes claro el concepto del dominio de una función polinómica (lineal, cuadrática, ...), función radical o racional puedes repasarlo en el recurso de Universo Fórmulas (Licencia CC). Y si tienes dudas sobre las herramientas generales y funcionalidades de Geogebra puedes acceder a su página de ayuda (Ayuda Geogebra). ...Àrea de coneixementContext educatiu
Licencia CC by Creative Commons El dominio de una función f(x) viene determinado por aquellos valores que puedo tomar la x para que exista la función. Si todavía no tienes claro el concepto del dominio de una función polinómica (lineal, cuadrática, ...), función radical o racional puedes repasarlo en el recurso de Universo Fórmulas (Licencia CC). Y si tienes dudas sobre las herramientas generales y funcionalidades de Geogebra puedes acceder a su página de ayuda (Ayuda Geogebra). ...Àrea de coneixementContext educatiu -
SdA: Simulando, que es gerundio
 Situación de Aprendizaje para que el alumnado diseñe simuladores de problemas de cinamática (MRU y MRUA)Àrea de coneixementContext educatiuTipus de recurs
Situación de Aprendizaje para que el alumnado diseñe simuladores de problemas de cinamática (MRU y MRUA)Àrea de coneixementContext educatiuTipus de recurs -
Situación de aprendizaje Cine en Casa
 Se propone a los alumnos recopilar información sobre los parámetros que debe cumplir una proyección cinematográfica según el estándar THX. Implementar estas recomendaciones en un espacio limitado lleva a la resolución de problemas matemáticos en los que se requiere el uso de trigonometría.Àrea de coneixementContext educatiuTipus de recurs
Se propone a los alumnos recopilar información sobre los parámetros que debe cumplir una proyección cinematográfica según el estándar THX. Implementar estas recomendaciones en un espacio limitado lleva a la resolución de problemas matemáticos en los que se requiere el uso de trigonometría.Àrea de coneixementContext educatiuTipus de recurs -
SdA Aprendemos Divisibilidad con juegos interactivos
 En esta situación de aprendizaje, explorarás los criterios de divisibilidad a través de actividades dinámicas y herramientas digitales como Genially, Educaplay, GeoGebra y Padlet. Trabajarás de forma individual y colaborativa, resolviendo problemas, creando recursos interactivos y evaluando tu progreso mediante cuestionarios y una diana de autoevaluación. El objetivo es reforzar tus conocimientos matemáticos mientras desarrollas competencias digitales y trabajas de manera activa y creativa.Àrea de coneixementContext educatiuTipus de recurs
En esta situación de aprendizaje, explorarás los criterios de divisibilidad a través de actividades dinámicas y herramientas digitales como Genially, Educaplay, GeoGebra y Padlet. Trabajarás de forma individual y colaborativa, resolviendo problemas, creando recursos interactivos y evaluando tu progreso mediante cuestionarios y una diana de autoevaluación. El objetivo es reforzar tus conocimientos matemáticos mientras desarrollas competencias digitales y trabajas de manera activa y creativa.Àrea de coneixementContext educatiuTipus de recurs -
Construyendo una ciudad
 Recurso para trabajar la Geometría en 3º de ESO a través del diseño y construcción de maquetas de edificios utilizando materiales reciclados.Àrea de coneixementContext educatiuTipus de recurs
Recurso para trabajar la Geometría en 3º de ESO a través del diseño y construcción de maquetas de edificios utilizando materiales reciclados.Àrea de coneixementContext educatiuTipus de recurs -
Jardinero Fiel
 REA de la asignatura de matemáticas de 4º de la ESO, secundaria en el que se trabaja la geometría analítica, estos conocimientos son el punto de partida que necesita el alumnado para avanzar en el proyecto. Trabajaremos con puntos, vectores, geometría del triángulo, rectas y sus posiciones. Con estas herramientas el alumnado deberá diseñar un jardín; se han creado unos personajes (Jacinto y Margarita) que proporcionan ayuda e interacción a lo largo de todo el recurso, haciendo una historia ...Àrea de coneixementContext educatiuTipus de recurs
REA de la asignatura de matemáticas de 4º de la ESO, secundaria en el que se trabaja la geometría analítica, estos conocimientos son el punto de partida que necesita el alumnado para avanzar en el proyecto. Trabajaremos con puntos, vectores, geometría del triángulo, rectas y sus posiciones. Con estas herramientas el alumnado deberá diseñar un jardín; se han creado unos personajes (Jacinto y Margarita) que proporcionan ayuda e interacción a lo largo de todo el recurso, haciendo una historia ...Àrea de coneixementContext educatiuTipus de recurs -
Fabricación de Parchís
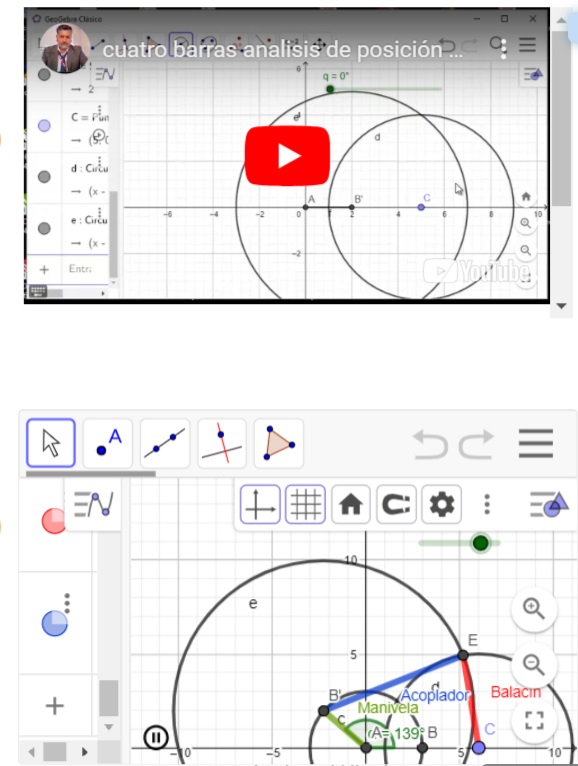 Los alumnos y alumnas deben fabricar un parchís compuesto de tablero, caja, figuras y dado. El reto consiste en realizar un mecanismo de cierre entre tablero y caja para poder almacenar las figuras dentro de la caja. Para ello necesitan conocimientos sobre los mecanismos de 4 barras estructurados en la Ley de Grashof. Gracias a la aplicación GeoGebra ha podido resolver el problema matemático de forma gráfica y eficiente. En el ámbito del aprendizaje de Mecanizado, la resolución de problema...Àrea de coneixementContext educatiuTipus de recurs
Los alumnos y alumnas deben fabricar un parchís compuesto de tablero, caja, figuras y dado. El reto consiste en realizar un mecanismo de cierre entre tablero y caja para poder almacenar las figuras dentro de la caja. Para ello necesitan conocimientos sobre los mecanismos de 4 barras estructurados en la Ley de Grashof. Gracias a la aplicación GeoGebra ha podido resolver el problema matemático de forma gráfica y eficiente. En el ámbito del aprendizaje de Mecanizado, la resolución de problema...Àrea de coneixementContext educatiuTipus de recurs -
Construimos una ciudad con geogebra
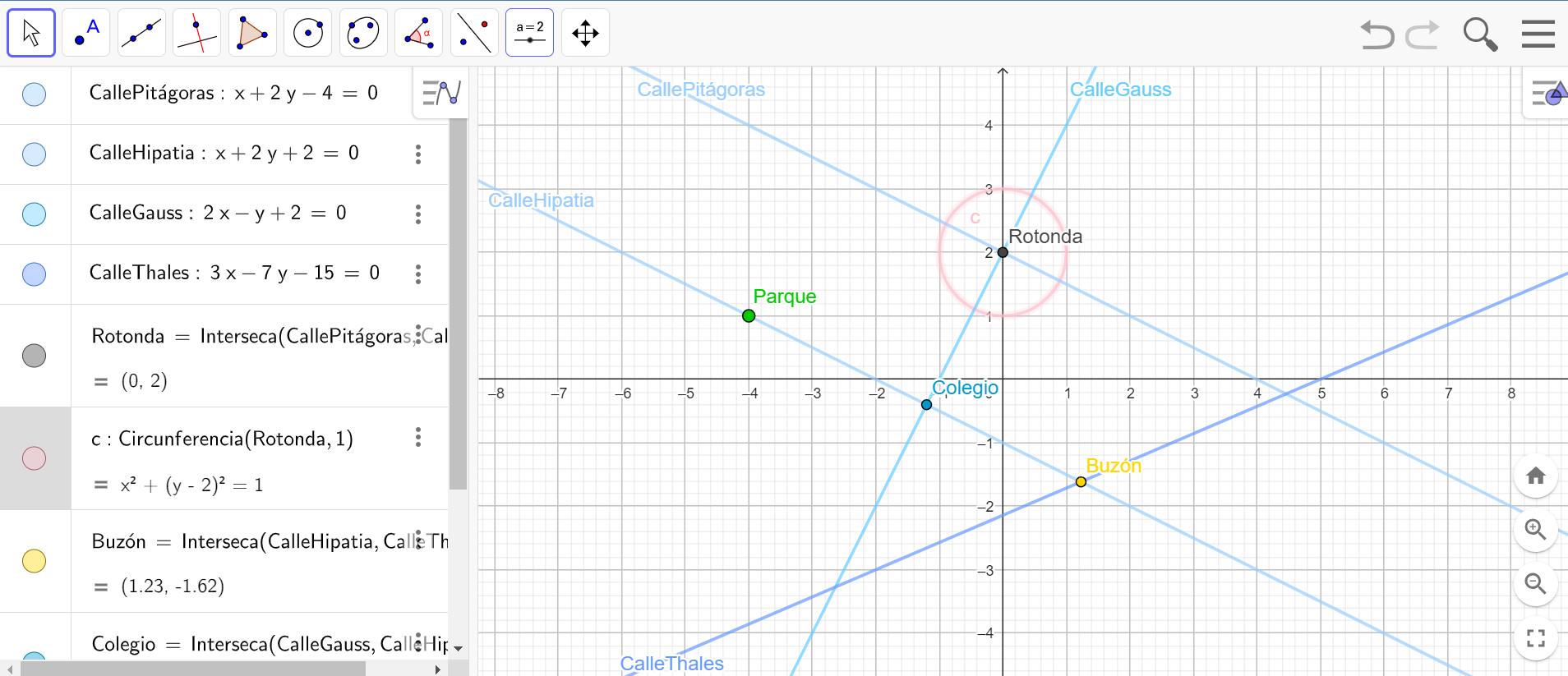 Este proyecto es el resultado del curso Competencia Digital B2, para mi especialidad, matemáticas. En él se encuentran todos los módulos trabajados unificados en eXeLearningÀrea de coneixementContext educatiuTipus de recurs
Este proyecto es el resultado del curso Competencia Digital B2, para mi especialidad, matemáticas. En él se encuentran todos los módulos trabajados unificados en eXeLearningÀrea de coneixementContext educatiuTipus de recurs -
Construyendo nuestra ciudad
 Este proyecto es el resultado del curso Competencia Digital B2, para mi especialidad, matemáticas. En él se encuentran todos los módulos trabajados unificados en eXeLearning.Àrea de coneixementContext educatiuTipus de recurs
Este proyecto es el resultado del curso Competencia Digital B2, para mi especialidad, matemáticas. En él se encuentran todos los módulos trabajados unificados en eXeLearning.Àrea de coneixementContext educatiuTipus de recurs -
La geometría que nos rodea con tecnología
 "La geometría que nos rodea con tecnología" es una situación de aprendizaje diseñada para explorar y comprender los conceptos geométricos presentes en el entorno utilizando herramientas tecnológicas. Esta situación de aprendizaje se centra en la aplicación práctica de la geometría en el mundo real, utilizando dispositivos como computadoras, tabletas, software de diseño gráfico, aplicaciones de realidad aumentada o dispositivos de medición láser. Los estudiantes se involucran en actividades...Àrea de coneixementContext educatiuTipus de recurs
"La geometría que nos rodea con tecnología" es una situación de aprendizaje diseñada para explorar y comprender los conceptos geométricos presentes en el entorno utilizando herramientas tecnológicas. Esta situación de aprendizaje se centra en la aplicación práctica de la geometría en el mundo real, utilizando dispositivos como computadoras, tabletas, software de diseño gráfico, aplicaciones de realidad aumentada o dispositivos de medición láser. Los estudiantes se involucran en actividades...Àrea de coneixementContext educatiuTipus de recurs -
Progresiones Aritméticas y Geométricas
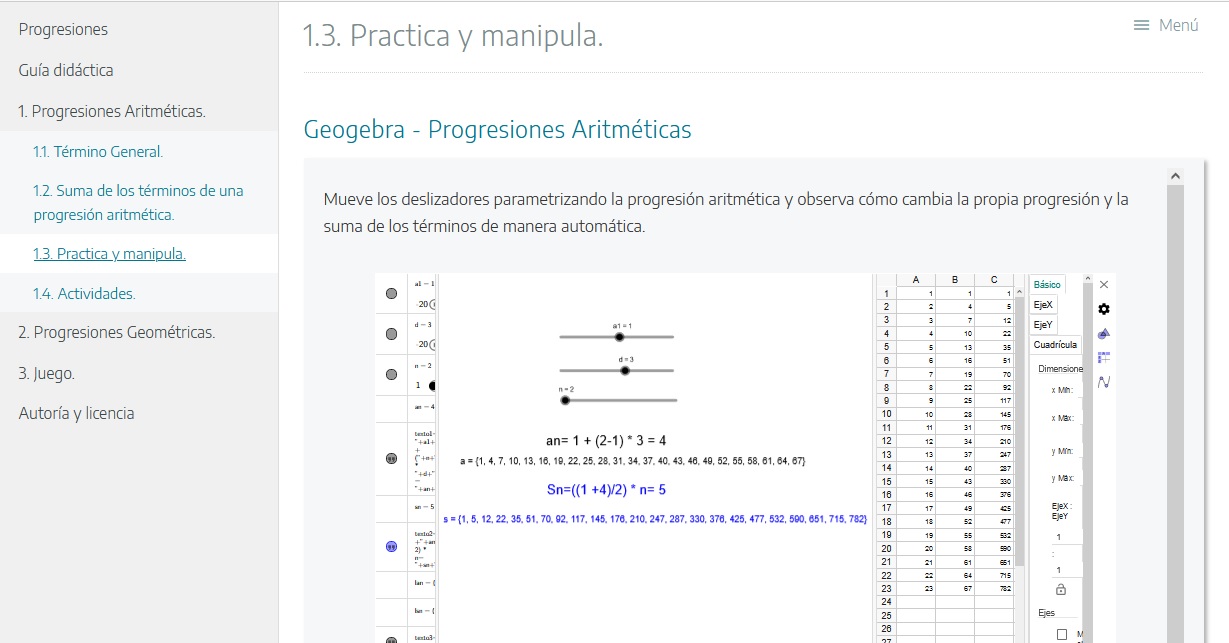 Nivel: 3º E.S.O. Asignatura: Matemáticas Académicas. Bloques de contenido: 1, 3 y 5.Àrea de coneixementContext educatiuTipus de recurs
Nivel: 3º E.S.O. Asignatura: Matemáticas Académicas. Bloques de contenido: 1, 3 y 5.Àrea de coneixementContext educatiuTipus de recurs -
La Geometría que nos rodea con Tecnología.
 La justificación de una situación de aprendizaje titulada "La geometría que nos rodea con tecnología" para estudiantes de segundo de la ESO se fundamenta en la integración de la tecnología como herramienta facilitadora del proceso de enseñanza-aprendizaje y en la relevancia de comprender los conceptos geométricos en el entorno cotidiano de los alumnos.Àrea de coneixementContext educatiuTipus de recurs
La justificación de una situación de aprendizaje titulada "La geometría que nos rodea con tecnología" para estudiantes de segundo de la ESO se fundamenta en la integración de la tecnología como herramienta facilitadora del proceso de enseñanza-aprendizaje y en la relevancia de comprender los conceptos geométricos en el entorno cotidiano de los alumnos.Àrea de coneixementContext educatiuTipus de recurs -
Estadística con Geogebra
 Situación de Aprendizaje basada en proyectos para trabajar estadística unidimensional incluyendo como recurso el software Geogebra.Àrea de coneixementContext educatiuTipus de recurs
Situación de Aprendizaje basada en proyectos para trabajar estadística unidimensional incluyendo como recurso el software Geogebra.Àrea de coneixementContext educatiuTipus de recurs


